Свойства гидростатического давления

Основы гидростатики

Как уже указывалось выше, в покоящейся жидкости возможен лишь один вид напряжений - напряжение сжатия, т.е. гидростатическое давление.

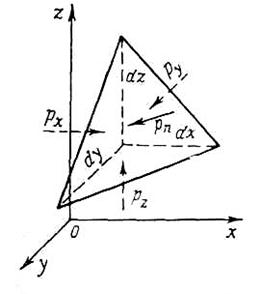
Рис. 2.1. Проекции сил давления

Необходимо иметь в виду следующие два свойства гидростатического давления в жидкости:

1. На внешней поверхности жидкости гидростатическое давление всегда направлено по нормали внутрь рассматриваемого объема жидкости.

Это свойство непосредственно вытекает из определения давления, как напряжения нормальной сжимающей силы.

Под внешней поверхностью жидкости следует понимать не только поверхности раздела ее с внешней средой, но и поверхности элементарных объемов, мысленно выделяемых нами из общего объема жидкости.

2. В любой точке внутри жидкости гидростатическое давление по всем направлениям одинаково, т.е. давление не зависит от угла наклона площадки, на которую оно действует в данной точке.

Для доказательства этого свойства выделим в неподвижной жидкости элементарный объем в форме прямоугольного тетраэдра с ребрами, параллельными координатным осям и соответственно равными dx, dy и dz (рис. 2.1).

Пусть вблизи выделенного объема на жидкость действует единичная массовая сила, составляющие которой равны X, Y и Z.

Обозначим через р_х гидростатическое давление, действующее на грань, нормальную к оси ох, через р_y - давление на грань, нормальную к оси оу, и т.д. Гидростатическое давление, действующее на наклонную грань, обозначим через р_n, а площадь этой грани - через dS. Все эти давления направлены по нормалям к соответствующим площадкам.

Составим уравнение равновесия выделенного объема жидкости сначала в направлении оси ох.

Проекция сил давления на ось ох равна

(2.1)

Масса тетраэдра равна произведению его объема на плотность, т.е. 1/6 dxdydzr; следовательно, массовая сила, действующая на тетраэдр вдоль оси ох, равна

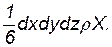
Уравнение равновесия тетраэдра запишется в следующем виде

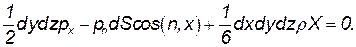
(2.2)

Разделим это уравнение на площадь - dy dz, которая представляет собой проекцию наклонной грани dS на плоскость yOz и, следовательно, равна

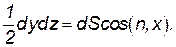
Будем иметь

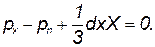
(2.3)

При стремлении размеров тетраэдра к нулю последний член уравнения, содержащий множитель dx, будет также стремиться к нулю, а давления р _х и р_n будут оставаться величинами конечными.

Следовательно, в пределе мы получим

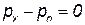
или

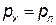
Аналогично составляя уравнения равновесия вдоль осей Оу и Oz, после таких же рассуждений получим

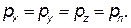
(2.4)

Так как размеры тетраэдра dx, dy и dz были взяты произвольно, то и наклон площадки dS произволен и, следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаково.

Это положение можно еще очень легко доказать, основываясь на формулах сопротивления материалов для напряжений при сжатии по двум и трем взаимно-перпендикулярным направлениям. Для этого достаточно положить в указанных формулах касательное напряжение равным нулю, и мы получим

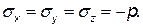
(2.5)

Доказанное свойство гидростатического давления в неподвижной жидкости имеет место также при движении невязкой жидкости. При движении же вязкой жидкости возникают касательные напряжения, вследствие чего гидромеханическое давление в вязкой жидкости указанным свойством, строго говоря, не обладает.