2014-02-05
1123
Теоретически решить задачу, связанную с движением жидкости возможно лишь для простейших случаем ламинарного движения. Во всех остальных случаях приходится прибегать в эксперименту.
В основу экспериментальных исследований заложена теория подобия. Теория гидродинамического подобия включает в себя геометрическое, кинематическое и динамическое подобие.
Геометрическое подобие – это пропорциональность сходственных размеров и равенство сходственных углов. Оно характеризуется масштабом геометрического подобия
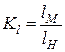, где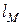 
- размер модели, 
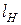- размер натуры
Кинематическое подобие – пропорциональность и одинаковая направленность скоростей сходственных точек геометрически подобных потоков. Характеризуется масштабом кинематического подобия.
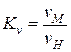
Динамическое подобие – это пропорциональность и одинаковая направленность сил, действующих на сходственные элементы кинематически и геометрически подобных потоков. Характеризуется динамическим коэффициентом подобия.
, 
, 
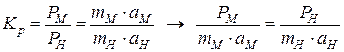
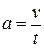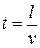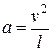
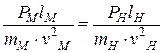
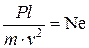– критерий Ньютона
|
|
|
Два потока подобны, если равны их критерии Ньютона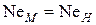 
Обеспечить подобие потоков по всем действующим силам практически невозможно. Как указывают эксперименты, подобие потоков будет обеспечено, если выполнено подобие по преобладающей в потоке силе.
Рассмотрим подобие 2х потоков, если преобладающей в них является сила тяжести –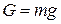 
.
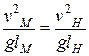
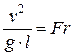– критерий Фруда
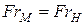
Рассмотрим подобие потоков, где преобладающими силами являются силы давления –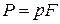 
.
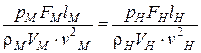
Если два потока геометрически подобны, то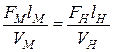 
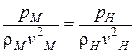
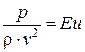- критерий Эйлера.
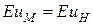
Рассмотрим подобие потоков, где преобладающими являются силы трения –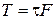 
.
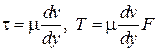
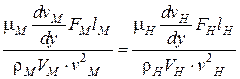
Для геометрически подобных потоков
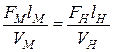
Для кинематически подобных потоков
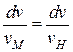
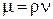
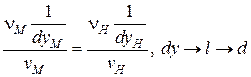
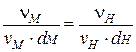
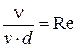- критерий (число) Рейнольдса.
Два потока будут подобны, если равных их числа Рейнольдса.
Каждый критерий представляет собой соотношение преобладающих в потока сил и сил инерции.
