2014-02-05
580
Общее выражение потерь напора на трение
Касательное напряжение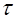 
в соответствии с формулой (4.13) распределяется по живому сечению потока по линейному закону (рис. 4).
Оно равно нулю на оси трубы (r =0) и принимает максимальное значение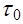 
на ее стенке (
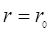), где
откуда следует, что
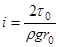, (5.14)
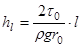. (5.15)
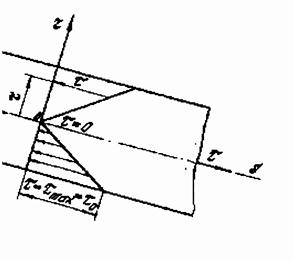
Рис.4
Уравнение (5.10) представляет собой общее выражение потерь напора при равномерном движении жидкости в трубопроводах круглого сечения.
В гидродинамике вместо касательного напряжения 
употребляют величину
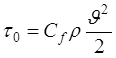, (5.16)
где Сf –коэффициент местного трения;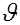 
–средняя скорость течения.
Подставляя в формулу (5.15) вместо его значение из формулы (5.16), получим
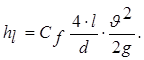(5.17)
Эта формула известна в литературе как формула Дарси-Вейсбаха.
Обозначив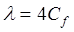 
, получим
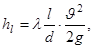(5.18)
где d – диаметр трубы.
Величина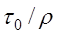 
имеет размерность квадрата скорости. Если ввести обозначение 
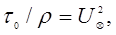где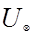 
–скорость касательного напряжения на стенке, или динамическая скорость, то уравнение (5.16) можно представить в виде
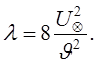(5.19)
Коэффициент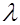 
, называемый коэффициентом гидравлического трения, имеет, очевидно, тот же смысл, что и 
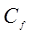. Важно выяснить, от каких параметров и как именно зависят эти коэффициенты.
Приведенный метод можно использовать также для определения вида формулы потерь напора на местные сопротивления. В этом случае, учитывая, что местные потери практически не зависят ни от длины участка трубы, ни от её диаметра, можно получить формулу
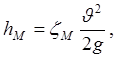(5.20)
где 
–безразмерный коэффициент, так называемый коэффициент местных потерь;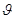
–средняя скорость потока после прохода через местное сопротивление.
Эта формула известна в литературе как формула Вейсбаха для местных сопротивлений.
Заметим, что к этому виду можно привести и формулу (18), если обозначить
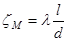. (5.21)
Тогда
.
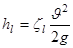Формула (5.20) применима для всех видов гидравлических сопротивлений, причем коэффициент сопротивления (или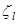 
) в наиболее общем случае зависит от конфигурации потока и числа Рейнольдса, Установление конкретного вида этих зависимостей в основном опирается на экспериментальные данные.
