2014-02-05
791
Рис.5
У стенок трубы (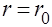
) скорость равняется нулю, на оси трубы (
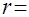0) скорость имеет максимальное значение, равное
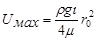. (5.28)
Расход жидкости в трубе можно найти путем суммирования элементарных расходов, проходящих через кольцевые площадки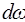 
радиусом 
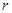и шириной 
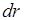(см. рис.3), т.е. из выражения
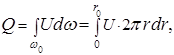
где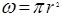 
; 
.
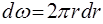После подстановки в выражение для Q вместо 
его значение из (5.27) получим
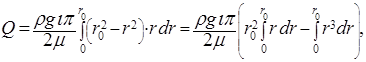
откуда после интегрирования найдем
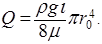(5.29)
Средняя скорость
(5.30)
Из сопоставления (5.29) и (5.30) видно, что
,
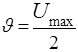следовательно, средняя скорость при ламинарном движении жидкости в трубе равна половине максимальной.
