Теорема Остроградского-Гаусса

Может показаться, что для выполнения условия (4.3) или (4.4) при удалении от источника должны возникать новые (или исчезать старые) линии. Однако это не так.

Рассмотрим поле точечного заряда 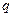. Модуль вектора напряженности поля точечного заряда 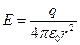. Проведем вокруг точечного заряда замкнутую поверхность (Рис.15). Элементарный поток через произвольную площадку 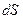будет 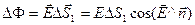, где 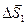– вектор, параллельный 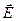, а, следовательно, и 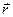, т.е. площадка 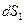, перпендикулярная радиусу-вектору, является элементом сферической поверхности радиуса 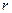. Тогда 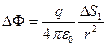, но 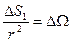– центральный телесный угол.

Полный поток поля, созданного точечным зарядом, через замкнутую поверхность будет 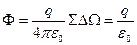. (4.5)

Как видим, полученный результат не зависит от положения заряда внутри полости, ограниченной поверхностью, а также не зависит от формы поверхности. Таким образом, полное число силовых линий, выходящих из точечного заряда 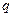, равно 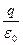и эти линии непрерывны на всем пути от заряда до бесконечности. Легко показать, что полученный результат справедлив для системы точечных зарядов.

Если внутри замкнутой поверхности находится несколько точечных зарядов, то полный поток будет равен сумме потоков, т.е. 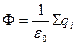или

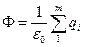. (4.6)

Таким образом, поток вектора напряженности электростатического поля 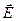через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на постоянную величину 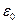. Соотношение (4.6) носит название теоремы Гаусса. Если алгебраическая сумма зарядов внутри замкнутой поверхности равна 0, т.е. заряженных частиц внутри поверхности нет или количество отрицательных зарядов численно равно количеству положительных, то полный поток вектора напряженности через такую поверхность будет равен нулю (рис.16).

В самом деле, любые два элементарных потока 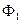и 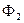через площадк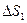и и 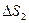равны по модулю, но знаки этих потоков противоположны, так как 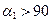, 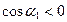и 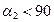, , 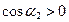следовательно, сумма их равна нулю. Этот вывод будет справедлив и для любых двух других участков замкнутой поверхности.

Теорема Гаусса математически эквивалентна закону Кулона, но ее часто удобнее использовать для расчетов электрических полей, созданных несколькими зарядами. Теорему Гаусса особенно удобно использовать для расчета полей, созданных заряженными телами или поверхностями, когда заряды распределены по поверхности или по объему равномерно или распределение подчиняется определенной симметрии.