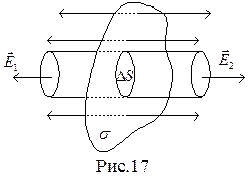Напряженность поля равномерно заряженной плоскости

Бесконечная плоскость заряжена равномерно с постоянной поверхностной плотностью 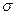положительным зарядом .

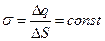Из соображения симметрии вытекает, что напряженность поля в любой точке имеет направление, перпендикулярное к плоскости. Если плоскость имеем конечные размеры, то этот вывод справедлив только для точек, расположенных вблизи поверхности плоскости и далеко от ее краев.

Далее очевидно, что в симметричных относительно плоскости точках напряженность поля одинакова по величине и противоположна по направлению .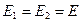

Выделим мысленно цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями величиной 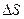, расположенными относительно плоскости симметрично (Рис.17).

Применим теорему Гаусса. Поток через боковую поверхность цилиндра равен нулю, линии напряженности параллельны образующей цилиндра.

Следовательно, суммарный поток через замкнутую поверхность цилиндра равен потоку через основания и по теореме Гаусса 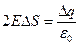, т.е.

. (4.7)

Полученный результат не зависит от положения точки в исследуемом поле, т.е. на любых расстояниях от бесконечной плоскости напряженность поля одинакова по величине. Поле, созданное заряженной плоскостью, однородно. Если плоскость заряжена отрицательным зарядом, то результат будет тот же, но вектор 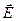и линии напряженности направлены к плоскости.