ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
Для более глубокого понимания электрических явлений необходимо количественно определить величину взаимодействия электрических зарядов. Выясним, как зависит величина силы, действующей на заряженное тело, расположенное рядом с другим заряженным телом, от величины разрядов на них. Для этого введем понятие точечного заряда, играющего в учении об электричестве такую же роль, как материальная точка в механике.
Точечным зарядом q называется наэлектризованное тело, размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми оно взаимодействует. В случае протяженных заряженных тел, размерами которых в данной задаче пренебречь нельзя, их следует мысленно разделить на достаточно малые заряженные элементы, каждый из которых можно было бы считывать точечным зарядом.
В 1785г. Шарль Кулон (1736-1806) опытным путем установил закон взаимодействия двух неподвижных точечных зарядов. Закон Кулона утверждает, что сила электростатического взаимодействия двух точечных зарядов прямо пропорциональна произведению величины этих зарядов и обратно пропорциональна квадрату расстояния между зарядами. Эта сила направлена вдоль прямой, соединяющей эти заряды (Рис.1).
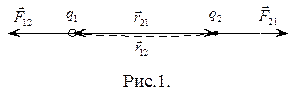
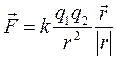 (2.1)
(2.1)
где вектор 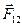 или
или 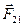 – вектор силы, действующей соответственно на заряд q1 или на заряд q2, эти векторы направлены вдоль радиуса-вектора
– вектор силы, действующей соответственно на заряд q1 или на заряд q2, эти векторы направлены вдоль радиуса-вектора 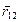 или
или 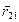 соответственно. Радиус-вектор
соответственно. Радиус-вектор 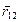 определяет положение заряда q1 относительно заряда q2, и
определяет положение заряда q1 относительно заряда q2, и 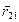 определяет положение заряда q2 относительно заряда q1, k – коэффициент пропорциональности, зависящий от выбора системы единиц измерения. В системе СИ за единицу измерения электрического заряда принят 1Кл = 1А·1с, где 1А и 1с – единица силы тока и единица времени – основные (эталонные) единицы измерения в Международной системе единиц (СИ).
определяет положение заряда q2 относительно заряда q1, k – коэффициент пропорциональности, зависящий от выбора системы единиц измерения. В системе СИ за единицу измерения электрического заряда принят 1Кл = 1А·1с, где 1А и 1с – единица силы тока и единица времени – основные (эталонные) единицы измерения в Международной системе единиц (СИ).
Тогда в системе СИ коэффициент пропорциональности 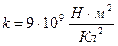 , коэффициент k часто выражают через другую постоянную величину
, коэффициент k часто выражают через другую постоянную величину 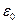 , называемую электрической постоянной.
, называемую электрической постоянной. 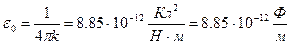 .
.
Тогда закон Кулона можно записать в форме
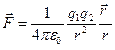 . (2.2)
. (2.2)
Закон, записанный в виде 2.1 или 2.2, позволяет определить как величину, так и направление вектора силы, действующей на один точечный заряд со стороны другого. Модуль силы взаимодействия можно определить следующим уравнением
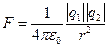 . (2.3)
. (2.3)
Если достаточно близко находится несколько точечных зарядов (заряженных тел), то каждая пара точечных зарядов взаимодействует друг с другом так, как будто других зарядов не существует. Например, заряд 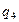 взаимодействует с другими (
взаимодействует с другими (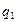 ,
,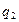 и
и 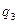 ) по закону Кулона (Рис.2). Результирующая сила, действующая на заряд
) по закону Кулона (Рис.2). Результирующая сила, действующая на заряд 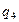 равна векторной сумме сил взаимодействия с каждым зарядом в отдельности
равна векторной сумме сил взаимодействия с каждым зарядом в отдельности 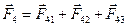 . Принцип суперпозиций для случая электростатических сил хорошо подтверждается экспериментально.
. Принцип суперпозиций для случая электростатических сил хорошо подтверждается экспериментально.
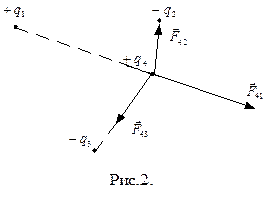
2.2. Примеры вычисления сил взаимодействия заряженных тел Пример 1. В трех вершинах квадрата находится три одинаковых по модулю и по знаку заряда 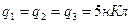 . Первый и третий – неподвижные. Какой величины и какого знака заряд
. Первый и третий – неподвижные. Какой величины и какого знака заряд 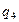 надо поместить в четвертой вершине квадрата, чтобы заряд
надо поместить в четвертой вершине квадрата, чтобы заряд 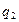 находился в равновесии? Как зависит ответ от длины стороны квадрата?
находился в равновесии? Как зависит ответ от длины стороны квадрата?
Решение: Чтобы заряд 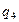 находился в равновесии, в четвертую вершину
находился в равновесии, в четвертую вершину
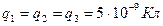 | квадрата надо поместить заряд (-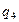 ) такой, чтобы ) такой, чтобы 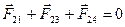 . . |
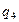 -? -? |

Как видно из (Рис.3)  . Но по закону Кулона
. Но по закону Кулона
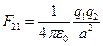 и
и 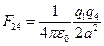 , где а – сторона квадрата. Тогда
, где а – сторона квадрата. Тогда 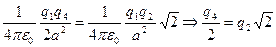 или
или 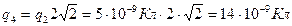
Ответ: 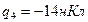 – величина заряда, который надо поместить в четвертую вершину квадрата, чтобы заряд
– величина заряда, который надо поместить в четвертую вершину квадрата, чтобы заряд 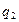 находился в равновесии, не зависит от длины стороны квадрата.
находился в равновесии, не зависит от длины стороны квадрата.
Пример 2. Три маленьких невесомых шарика соединены невесомыми и нерастяжимыми нитями длиной 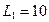 см и
см и 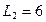 см. Шарикам сообщают одинаковые и одноименные заряды по 1 мкКл. Каковы после этого силы натяжения каждой из нитей?
см. Шарикам сообщают одинаковые и одноименные заряды по 1 мкКл. Каковы после этого силы натяжения каждой из нитей?

Рис. 4.
| Решение: Система трех заряженных тел связанных нитями, находится в | |
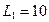 см. см. 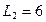 см см 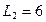 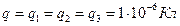 | равновесии когда сумма сил, действующих на каждый заряд, равны нулю, т.е. |
 -? -?  -? -? |
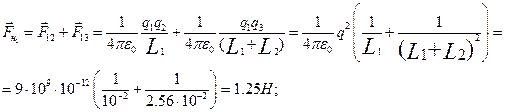
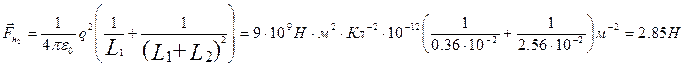
Ответ: 1,25Н; 2,85Н.
Пример 3. Два точечных заряда, расположенные на расстоянии 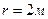 друг от друга взаимодействуют с силой
друг от друга взаимодействуют с силой 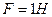 . Их суммарный заряд
. Их суммарный заряд 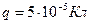 . Каковы величины
. Каковы величины 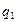 и
и 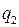 этих зарядов?
этих зарядов?
Решение: По закону Кулона 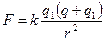 . Откуда . Откуда 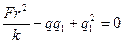 . . | |
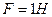 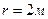 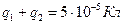 | Решая это квадратное уравнение, получим 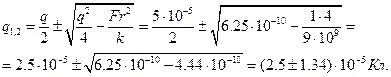 |
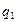 -? -? 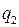 -? -? |
Ответ: 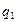 = 3,84·10-5Кл,
= 3,84·10-5Кл, 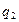 = 1,16·10-5Кл.
= 1,16·10-5Кл.
Пример 4. Точечные заряды 1 и 2 закреплены. Заряд 3 может перемещаться (Рис.5).
| 1. с ускорением влево; 2. равномерно влево; 3. остается в покое; 4. равномерно вправо, 5. с ускорением вправо. | 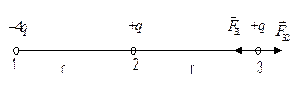 Рис.5. Рис.5. |
Решение: Для выбора правильного ответа необходимо вычислить силу, действующую на третий заряд со стороны первого и второго зарядов. Результирующая сила, действующая на третий заряд, будет 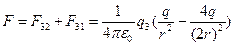 . Как видно эта сила равна нулю. Следовательно третий заряд будет находится в покое.
. Как видно эта сила равна нулю. Следовательно третий заряд будет находится в покое.
Ответ: 3.
 2014-02-02
2014-02-02 4777
4777