 Определение. Функция
Определение. Функция 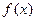 называется бесконечно большой величиной при
называется бесконечно большой величиной при 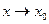 , если для любого, даже сколь угодно большого положительного числа М>0, найдется такое положительное число
, если для любого, даже сколь угодно большого положительного числа М>0, найдется такое положительное число  >0 (зависящее от М,
>0 (зависящее от М, 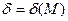 ), что для всех х, не равных
), что для всех х, не равных 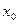 и удовлетворяющих условию
и удовлетворяющих условию <
< , будет верно неравенство
, будет верно неравенство
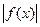 > М (5.3.9)
> М (5.3.9)
Запись того, что функция 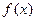 бесконечно большая при
бесконечно большая при 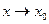 , следующая:
, следующая:
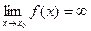 или
или 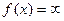 при
при 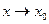 .
.
Это же определение можно представить в виде:
(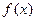 -бесконечно большая величина при
-бесконечно большая величина при 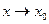 , или
, или 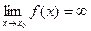 )
)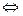
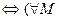 >0)
>0) 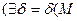 >0) (
>0) (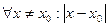 <
< )
) 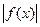 > М.
> М.
Если в приведенном определении 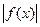 > М (или
> М (или 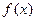 <- М), то пишут
<- М), то пишут 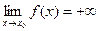 (или
(или 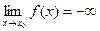 ).
).
Аналогично можно было определить понятие бесконечно большой величины при 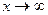 . Приведем его в краткой форме:
. Приведем его в краткой форме:
(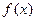 - бесконечно большая величина при
- бесконечно большая величина при 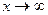 , или
, или 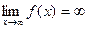 )
) 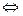
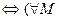 >0)
>0) 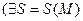 >0) (
>0) (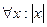 > S)
> S) 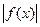 > М.
> М.
Пример. Доказать, что функция 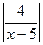 является бесконечно при
является бесконечно при 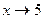 .
.
Выберем сколь угодно большое М>0.
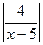 >М, если
>М, если 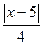 <
<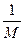 , или
, или 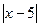 <
<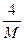 . Действительно, найдется такое
. Действительно, найдется такое 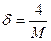 , что если
, что если 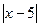 <
< , то верно неравенство
, то верно неравенство 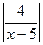 >М. Если М=1000, то
>М. Если М=1000, то 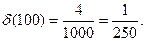
Замечание 1. Не следует путать бесконечно большую переменную величину 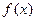 с очень большим, но постоянным числом М>0, ибо по мере приближения значений х к
с очень большим, но постоянным числом М>0, ибо по мере приближения значений х к 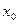 (при
(при 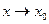 ) или по мере увеличения по модулю х (при
) или по мере увеличения по модулю х (при 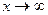 ) в соответствии с неравенством (5.3.9) функция
) в соответствии с неравенством (5.3.9) функция 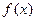 превзойдет это число М(по абсолютной величине).
превзойдет это число М(по абсолютной величине).
Замечание 2. не следует путать понятия бесконечно большой величины и неограниченной величины. Всякая неограниченная функция при 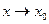 не всегда является бесконечно большой. В то время как бесконечно большая величина при
не всегда является бесконечно большой. В то время как бесконечно большая величина при 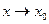 всегда неограниченная величина.
всегда неограниченная величина.
 2014-02-05
2014-02-05 753
753








