Теорема 5.3.1. Если функция 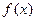 имеет вид
имеет вид 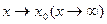 предел, равный А, то её можно представить в виде суммы этого числа А и бесконечно малой величины
предел, равный А, то её можно представить в виде суммы этого числа А и бесконечно малой величины 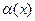 при
при 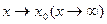 .
.
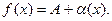 (5.3.8)
(5.3.8)
Докажем теорему для случая 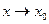 . По условию
. По условию 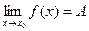 . Это означает, что для любого
. Это означает, что для любого 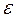 >0 существует такое число
>0 существует такое число  >0, что для всех
>0, что для всех  и удовлетворяющий условию
и удовлетворяющий условию  <
< , будет верно неравенство
, будет верно неравенство 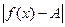 <
<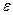 , или, обозначив
, или, обозначив 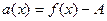 , справедливо неравенство
, справедливо неравенство 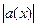 <
<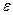 . Это и означает, что
. Это и означает, что 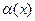 есть бесконечно малая величина при
есть бесконечно малая величина при 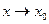 .
.
 2014-02-05
2014-02-05 1230
1230








