1. Волны де-Бройля. К двадцатым годам ХХ века в физике окончательно утвердилось понимание того факта, что свет имеет двойственную природу. В таких явлениях, как интерференция, дифракция, поляризация свет ведёт себя как волна, а в явлениях фотоэффекта и эффекта Комптона свет ведёт себя как поток частиц.
В корпускулярном проявлении каждая световая частица – фотон – характеризуется двумя величинами: энергией hn и импульсом hnçс. Если свет ведёт себя как волна, он описывается уравнением плоской монохроматической волны  . Физический смысл величины Е зависит от того, в какой модели рассматривается свет. В эфирной модели Е – это смещение частиц эфира относительно положения равновесия. В ЭМ модели Е – это напряжённость электрического поля в точках оси ОХ в моменты времени t.
. Физический смысл величины Е зависит от того, в какой модели рассматривается свет. В эфирной модели Е – это смещение частиц эфира относительно положения равновесия. В ЭМ модели Е – это напряжённость электрического поля в точках оси ОХ в моменты времени t.
В 1924 г. француз Луи де-Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм (двойственность) присущ не только микрообъектам полевой формы материи (фотонам), но и микрообъектам, которые традиционно понимались до этого как частицы (масса покоя не равна нулю). То есть к электронам, ядрам, атомам. Иначе, дуализм есть универсальное свойство материи.
По мысли де-Бройля, каждой так называемой частице для описания её волновых свойств нужно поставить в соответствие некоторую волновую функцию ψ (как функцию Е, соответствующую фотону). Эта функция ψ (функция пси де-Бройля) также описывает плоскую монохроматическую волну, распространяющуюся в направлении скорости v движения частицы. Хотя физический смысл функции ψ оставался ещё неясным, тем не менее, к корпускулярным характеристикам частицы – энергии и импульсу – можно было добавить по аналогии некоторые волновые. Например, длину волны.
Импульс фотона 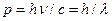 . Отсюда, длина волны фотона с импульсом p есть
. Отсюда, длина волны фотона с импульсом p есть 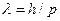 . Применительно к частице её импульс p = mv. Отсюда
. Применительно к частице её импульс p = mv. Отсюда
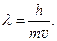 Длина волны де-Бройля (3.1)
Длина волны де-Бройля (3.1)
Чем больше импульс частицы, тем меньше дебройлевская длина волны. Например, для электрона, ускоренного разностью потенциалов 100 В, λ = 0,12 нм, для протона при тех же условиях λ = 0,003 нм.
Идею волновых свойств микрочастиц де-Бройль использовал для объяснения правила квантования орбит в атоме Бора. Он предположил, что стационарными орбитами электронов в атоме водорода являются те, на которых укладывается целое число длин волн де-Бройля.
Если движение электрона по орбите рассматривать как волну материи, то на стационарной орбите волна при обходе ядра будет всякий раз возвращаться в исходную точку с той же фазой и амплитудой. В каждой точке орбиты установится постоянный колебательный режим, и потому не возникнет излучения (как в замкнутом идеальном колебательном контуре). Условие квантования принимает вид: 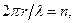 где n = 1, 2, 3,... (3.2)
где n = 1, 2, 3,... (3.2)
Здесь r – радиус круговой орбиты. Так как 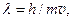 то
то 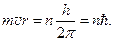 (3.3)
(3.3)
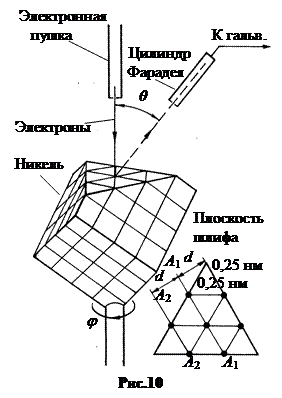 2. Дифракция электронных пучков в опытах Девиссона-Джермера. В 1927 г. американцы Клинтон Девисон и Лестер Джермер исследовали отражение электронов от монокристалла никеля. Установка включала в себя монокристалл никеля, сошлифованный, как показано на рис.10, и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением U на электронной пушке:
2. Дифракция электронных пучков в опытах Девиссона-Джермера. В 1927 г. американцы Клинтон Девисон и Лестер Джермер исследовали отражение электронов от монокристалла никеля. Установка включала в себя монокристалл никеля, сошлифованный, как показано на рис.10, и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением U на электронной пушке:
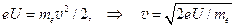 .
.
Под углом θ к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме.
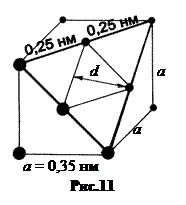 Металлический никель (Ni, Z = 28, Mr = 58,7) может существовать в двух кристаллических модификациях (α и β). Обычное состояние – β -модификация, кубическая гранецентрированная решётка с постоянной а = 0,35 нм. Если у кристалла срезать угол, как показано на рис.10, то атомы в плоскости цилиндра приобретают ось симметрии 3-го порядка. Это значит, что при повороте кристалла на угол φ = 120° атомы в плоскости цилиндра принимали тождественное положение. Расстояние между атомами в плоскости шлифа равно
Металлический никель (Ni, Z = 28, Mr = 58,7) может существовать в двух кристаллических модификациях (α и β). Обычное состояние – β -модификация, кубическая гранецентрированная решётка с постоянной а = 0,35 нм. Если у кристалла срезать угол, как показано на рис.10, то атомы в плоскости цилиндра приобретают ось симметрии 3-го порядка. Это значит, что при повороте кристалла на угол φ = 120° атомы в плоскости цилиндра принимали тождественное положение. Расстояние между атомами в плоскости шлифа равно 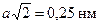 (рис.11).
(рис.11).
В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния θ (0 < θ < 90°), от азимутального угла j (0 ≤ j ≤ 360°), от скорости v электронов в пучке.
Электроны, падающие на кристалл, при энергиях не более 80 эВ не проникают внутрь. Они отражаются от плоскости шлифа как свет от отражательной дифракционной решётки. Штрихи решётки формируются рядами атомов А 1 А 2... Расстояние между рядами (постоянная решётки) 
Опыты показали, что имеется ярко выраженная селективность рассеяния электронов. Первый максимум наблюдался при углах 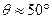 . При изменении азимутального угла φ максимумы повторялись через 120°.
. При изменении азимутального угла φ максимумы повторялись через 120°.
Рассмотрим в качестве примера следующие данные. При напряжении на электронной пушке U = 54 В первый максимум интенсивности наблюдался под углом 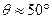 . Если бы под таким углом дифрагировал на решётке свет, то его длина волны λ нашлась бы из условия главных максимумов:
. Если бы под таким углом дифрагировал на решётке свет, то его длина волны λ нашлась бы из условия главных максимумов: 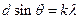 . При k = 1
. При k = 1 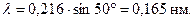
Длина волны де-Бройля для электронов равна
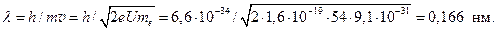
Гипотеза де-Бройля нашла опытное подтверждение.
3. Дифракция электронных пучков в опытах Дж. П. Томсона. В 1928 г. Джордж Паджет Томсон (сын Дж. Дж. Томсона, открывшего в 1897 г. электрон) поставил опыт по дифракции электронных пучков при прохождении их через металлическую фольгу.
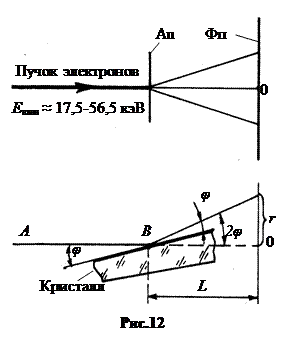 Узкий моноэнергетический пучок электронов направлялся из электронной пушки на листок очень тонкой золотой фольги толщиной около 0,1 мкм. Чтобы электроны меньше поглощались и могли проходить сквозь фольгу, они разгонялись в электрическом поле с напряжением U в несколько десятков киловольт. Рассеянные на фольге электроны попадали на фотопластинку ФП (рис.12, вверху).
Узкий моноэнергетический пучок электронов направлялся из электронной пушки на листок очень тонкой золотой фольги толщиной около 0,1 мкм. Чтобы электроны меньше поглощались и могли проходить сквозь фольгу, они разгонялись в электрическом поле с напряжением U в несколько десятков киловольт. Рассеянные на фольге электроны попадали на фотопластинку ФП (рис.12, вверху).
Опыты показали, что после проявления экспонированной в электронном пучке фотопластинки на ней появлялись концентрические тёмные кольца. Механизм их появления можно объяснить так.
Полученная по обычной технологии из отливки и прокатанная золотая фольга состоит из множества мелких хаотично ориентированных кристалликов размером около 0,01 мкм. На пути электронного пучка оказывается множество граней таких кристалликов со всевозможной ориентацией. В одних случаях электрон проходит сквозь такой микрокристалл, в других – упруго отражается от него. В результате возникает хаотическое рассеяние электронов, создающее диффузное потемнение фотопластинки. Но в тех случаях, когда грань кристалла образует с осью падающего электронного пучка угол скольжения φ, соответствующий дифракционному максимуму по формуле Вульфа-Брэгга 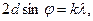 (3.4)
(3.4)
 где d – расстояние между атомными плоскостями, в направлении угла 2 φ в рассеянном пучке реализуется дифракционный максимум (рис.12, внизу). Как и рентгеновские пучки, электроны дифрагируют на атомных плоскостях, параллельных грани кристалла. В направлении угла 2 φ на фотопластинке на фоне вялого диффузного потемнения образуется от грани кристалла интенсивное чёрное пятно.
где d – расстояние между атомными плоскостями, в направлении угла 2 φ в рассеянном пучке реализуется дифракционный максимум (рис.12, внизу). Как и рентгеновские пучки, электроны дифрагируют на атомных плоскостях, параллельных грани кристалла. В направлении угла 2 φ на фотопластинке на фоне вялого диффузного потемнения образуется от грани кристалла интенсивное чёрное пятно.
Множество таких кристалликов благодаря осевой симметрии относительно пучка АО образуют в статистике концентрические кольца (рис.13). Если радиус кольца r, а расстояние от фольги до фотопластинки L, то, учитывая малость значений углов φ, можно записать равенство 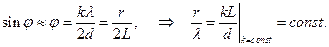 (3.5)
(3.5)
Изменяя напряжение U в электронной пушке, можно менять скорость электронов v и, тем самым, соответствующую электронам дебройлевскую длину волны λ. Радиус r кольца будет меняться. Но согласно (3.5), при сохранении геометрии установки неизменной (L = const) отношение rçλ для одного и того же кольца будет оставаться постоянным.
Измерения показали, что отношение rçλ в опытах действительно сохраняется.
В опытах Девиссона-Джермера использовались пучки относительно медленных электронов, которые разгонялись в поле напряжением U не более 100 В. Их скорость вычислялась по классической формуле eU = mv 2 ç 2 и не превышала 2% от скорости света.
В опытах Томсона использовались пучки электронов высоких энергий
(E кин ≈ 17,5-56,5 кэВ). Для вычисления их скорости должна использоваться релятивистская формула кинетической энергии.
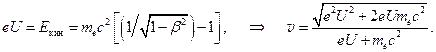 (3.6)
(3.6)
Здесь β = vçс, 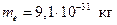 – масса покоя электрона (здесь и везде).
– масса покоя электрона (здесь и везде).
Например, в одном из опытов было U = 54,3 кВ. Скорость электронов, вычисленная по формуле (3.6), равна 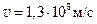 , что около половины скорости света с.
, что около половины скорости света с.
Для вычисления длины волны де-Бройля в формулу 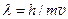 нужно подставлять релятивистскую массу электрона
нужно подставлять релятивистскую массу электрона 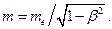 В нашем примере длина
В нашем примере длина 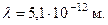
Поскольку электроны в опытах Томсона имеют энергию десятки кэВ, то при их торможении на фольге могут генерироваться рентгеновские лучи. Поэтому возникает опасение, что картина на фотопластинке образуется дифракцией Х -лучей. Для устранения сомнений Томсон создавал перед фотопластинкой магнитное поле. В результате картина, создаваемая электронами, смазывалась. Таким путём можно всегда отличить электронные дифракционные кольца от колец рентгеновских лучей.
Итак, опыты Томсона показали, что при рассеянии электронов на тонкой металлической фольге они (электроны) проявляют волновые свойства с длиной волны де-Бройля.
4. Дифракция отдельных электронов. Опыты Дэвиссона-Джермера и Томсона подтвердили формулу дебройлевской длины волны (3.1). Однако эти опыты были выполнены с электронными пучками больших интенсивностей, в которых концентрация электронов была настолько велика, что их нельзя было считать системой невзаимодействующих частиц. Поэтому оставалось допущение, что дифракция электронного пучка есть свойство коллектива электронов, а не отдельных электронов.
Чтобы снять сомнения, Л. Биберман, Н. Сушкин и В. Фабрикант в 1949 г. поставили опыт с электронными пучками столь малых интенсивностей, что электроны проходили через мишень заведомо поодиночке. Паузы были в 30000 раз продолжительнее времени прохождения электрона. Результаты опытов вновь подтвердили формулу де-Бройля.
5. Соотношение неопределённостей Гейзенберга. Из анализа накопленного к концу двадцатых годов экспериментального материала следовало, что есть явления, в которых электроны ведут себя как частицы. Это, например, движение электронов в электронно-лучевых трубках, в камере Вильсона. Здесь их движение может быть описано в понятиях классической механики, а сами электроны могут моделироваться материальными точками.
Но есть такие явления, в которых положение электронов в пространстве определяются вероятностными законами. Это, например, рассеяние электронов на кристаллах. Здесь нельзя говорить о траекториях их движения, поскольку исчезает механическая однозначность в поведении микрообъектов. Если рассмотреть дифракционные кольца на фотопластинках в опытах Томсона под микроскопом, то все эти кольца распадаются на кольцевые системы точечных почернений. Каждая черная микроточка образуется при поглощении единичного электрона. Таким образом, отдельный электрон никаких дифракционных колец не дает, он поглощается как частица.
Дифракционные кольца образуются разной густотой электронных следов. В местах дифракционных максимумов их густота больше, в местах минимумов – меньше. В какую точку попадёт электрон, сказать однозначно нельзя.
На вопрос: каковы критерии применимости классической или квантовой модели – ответил в 1927 г. немец Вернер Гейзенберг. Он открыл соотношение неопределённостей для координаты и импульса микрочастиц.
Он рассуждал примерно так. Чтобы определить положение и импульс электрона, нужно осветить его и получить хотя бы один рассеянный при столкновении фотон. Вследствие дифракции погрешность определения координаты электрона не может быть меньше длины волны фотона, ∆x ≈ λ. Чем точнее нужно определить положение электрона, тем меньше должно быть λ, тем более жёстким будет фотон. При столкновении с фотоном электрон получает отдачу, которая тем больше, чем больше импульс фотона hçλ. Итак, уменьшая погрешность в координате ∆x, мы увеличиваем погрешность в импульсе ∆рx, и наоборот.
Обычно соотношение неопределённостей записывают для проекций импульса и координат.
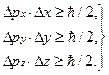
Соотношение неопределённостей для координат – импульса. (3.7)
Гейзенберг, 1927 г.
Здесь ∆ р и ∆ х, ∆ y, ∆ z – среднеквадратичные отклонения величин от их средних значений.
Из соотношения неопределённостей следует, что чем точнее определена одна из входящих в неравенство величин, тем менее определённым становится значение другой. Никакой эксперимент не может дать одновременно точные значения координаты и импульса микрочастицы.
Что касается макроскопических тел, то их импульсы настолько велики по сравнению с квантовыми неопределённостями, что могут быть измерены с любой практически мыслимой точностью, как и их координаты. Можно показать, что даже движение газовых молекул при температурах, достаточно далёких от абсолютного нуля, можно рассматривать как движение классических частиц.
Дальнейшее развитие квантовой механики показало, что суть соотношения неопределённостей не в том, что несовершенны измерительные системы. Суть в том, что неопределённость координаты и импульса есть объективное свойство материи. Соотношение неопределённостей Гейзенберга указывает границы корректности вопросов, которые можно задавать природе.
Соотношение неопределённостей можно записать еще для двух величин – энергии Е и времени t: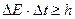 . (3.8)
. (3.8)
Если система находится в стационарном состоянии, то есть в состоянии, которое при отсутствии внешних сил не меняется, то энергию системы в этом состоянии можно измерить точно. Так, мы точно знаем стационарные уровни энергии в атомах.
Если же система не стационарна, то неопределённость значения энергии не может быть меньше hç ∆ t, где ∆ t – характерное время, в течение которого система может существовать в неустойчивом состоянии.
6.Микрочастицы и принцип наглядности. С развитием квантовой физики пришлось отказаться от наглядности физических моделей. Рассмотрим мысленный эксперимент по дифракции электронов на двух отверстиях. Мысленный потому, что диаметр отверстий должен быть одного порядка с диаметром атома водорода, что технически трудно сделать. Однако дифракция электронов на атомных плоскостях показывает, что события должны развиваться именно так.
Рассмотрим дифракцию электронов по схеме Юнга. На пути электронного пучка находится экран Э1 с двумя отверстиями 1 и 2. Далее по ходу движения электронов находится экран Э2 с фотопластинкой ФП (рис.14, вверху).
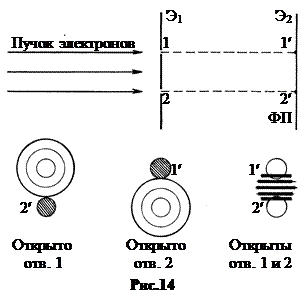 Мысленно представим, что электроны поодиночке проходят через 1-е отверстие
Мысленно представим, что электроны поодиночке проходят через 1-е отверстие
(2-е закрыто) и формируют на фотопластинке дифракционную картину в виде колец с центром в точке 1′ проекции отверстия 1 (рис.14, внизу слева). Если закрыть 1-е и открыть 2-е отверстие, то на фотопластинке также возникнет дифракционная картина в виде колец с центром в точке 2′ проекции отверстия 2 (рис.14, внизу в середине).
Если же открыть оба отверстия, то получится не сумма дифракционных картин отдельных отверстий, а дифракционная картина на двух отверстиях сразу (рис.14, внизу справа). Получается, что каждый электрон проходит одновременно через оба отверстия. В то же время во всех явлениях электрон – целостный не дробящийся объект. Ситуация ненаглядна. Но это объективное свойство квантовых моделей.
 2014-02-02
2014-02-02 6942
6942
