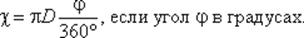Уравнение количества движения
Модель идеальной жидкости
Основные понятия о движении жидкости
5.4. Уравнение Бернулли для идеальной жидкости
5.5. Уравнение Бернулли для реальной жидкости
5.6. Измерение скорости потока и расхода жидкости
5.7. Уравнение энергии в дифференциальной форме
Гидродинамика - раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.
Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы - круг (рис.5.1, а); живое сечение клапана - кольцо с изменяющимся внутренним диаметром (рис.5.1, б).

Рис. 5.1. Живые сечения: а - трубы, б - клапана
Смоченный периметр 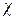 ("хи") - часть периметра живого сечения, ограниченное твердыми стенками (рис.5.2, выделен утолщенной линией).
("хи") - часть периметра живого сечения, ограниченное твердыми стенками (рис.5.2, выделен утолщенной линией).
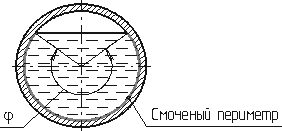
Рис. 5.2. Смоченный периметр
Для круглой трубы, если угол в радианах,
|
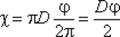
|
|
если угол в градусах.
|
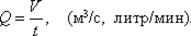
Средняя скорость потока υ - скорость движения жидкости, определяемая отношением расхода жидкости Q к площади живого сечения ω
|
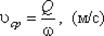
Понятие средней скорости вводят, поскольку скорость движения различных частиц жидкости отличается друг от друга. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.
Гидравлический радиус потока R - отношение живого сечения к смоченному периметру
|
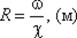
Течение жидкости может быть установившимся и неустановившимся.
Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени.
|
P = φ f(x, y, z)
Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным.
|
P = φ f1(x, y, z, t)
Линия тока это кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.
Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Рис. 5.3. Линия тока и струйка тока
Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное - течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.).
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.5.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q1=Q2= const, откуда
|
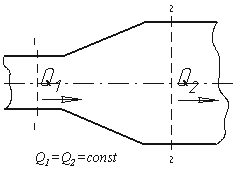
Рис. 5.4. Труба с переменным диаметром при постоянном расходе
|
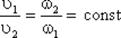
Уравнение неразрывности в гидродинамике - одно из уравнений, выражающее закон сохранения массы для любого объёма движущейся жидкости (газа). Оно может быть представлено не только в интегральном виде (5.8, 5.9), но и в дифференциальном. В переменных Эйлера уравнение неразрывности имеет вид:
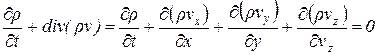 (5.10)
(5.10)
где r — плотность жидкости, v — её скорость в данной точке, a vx, vy, vz — проекции скорости на координатные оси. Если жидкость несжимаема (r = const), уравнение неразрывности принимает вид:
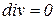 или
или 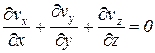 (5.11)
(5.11)
Движение жидкости, сопровождающееся вращением частиц вокруг осей, через них проходящих, называется вихревым движением. Для вихревого движения угловая скорость вращения не должна быть равна нулю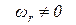 . Безвихревое (потенциальное) движение возможно, если соблюдаются условие
. Безвихревое (потенциальное) движение возможно, если соблюдаются условие
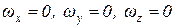
 2014-02-02
2014-02-02 1737
1737