Лекция № 3. Основные вопросы, рассматриваемые на лекции

Тема: Функции. ВЫБОРКИ

Основные вопросы, рассматриваемые на лекции:

1. Соответствия между множествами.

2. Функции и их графики.

3. Выборки из n элементов по m.

4. Математическое представление выборок.

Краткое содержание лекционного материала

1. Соответствия между множествами. Подмножество 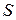декартова произведения 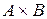называется соответствием между множествам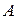и и 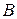. При этом пишут 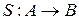. Если , то пишут 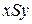и говорят, что элементу 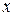поставлен в соответствие элемент .

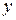Соответствие 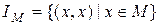называется тождественным отображением на множестве M.

Пусть дано соответствие 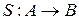. Соответствие 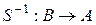называется обратным к соответствию 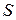, если .

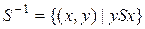Пусть заданы два соответствия: 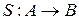и 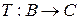. Композицией соответстви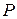й и 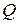называется соответствие 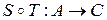, определенное следующим образом: .

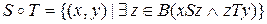Существует два вида соответствий: всюду определенные и однозначные.

Соответствие 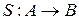называется всюду определенным, если выполняется следующее условие: .

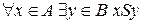Соответствие 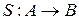называется однозначным, если выполняется следующее условие: .

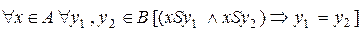Всюду определенное и однозначное соответствие 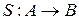называется отображением множества 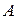в множество .

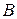2. Функции и их графики. Однозначное соответствие 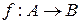называется также функцией. При этом вместо записи 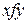пишут 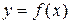. Путаницы не возникает, так как для любого 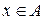существует не более одного 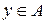, такого, что 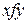. Если для некоторого 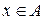не существует 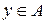, такого, что 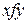, то говорят, что 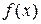не определено.

Графиком функции 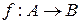называется множество

.

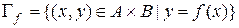Существует два вида отображений: инъекции и сюръекции.

Отображение 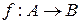называется сюръекцией, или отображением множества 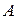на множество 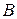, если .

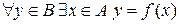Отображение 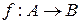называется инъекцией, или взаимно однозначным отображением множества 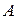в множество 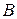, если

.

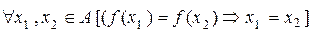Отображение 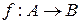, которое одновременно является и инъекцией, и сюръекцией, называется биекцией, или взаимно однозначным отображением множества 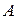на множество .

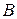3. Выборки из n элементов по m. Комбинации, или выборки, – это различные конструкции элементов заданного множества, подчиненных тем или иным условиям. Простейшие из них – это выборки из n элементов по m, построения, в которых из заданного n -множества надо выбрать элементы m раз, упорядоченных или неупорядоченных, с повторениями или без повторений.

Размещения из n элементов по m – это упорядоченные выборки элементов из заданного n -множества по m.

Приведем все размещения из 3 элементов множества 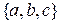по 2.

С повторениями: .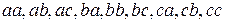

Без повторений: .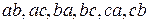

Приведем все размещения из 2 элементов множества 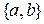по 3.

С повторениями: .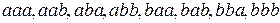

Сочетания из n элементов по m – это неупорядоченные выборки элементов из заданного n -множества по m.

Приведем все сочетания из 3 элементов множества 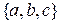по 2.

С повторениями: .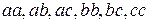

Без повторений: .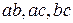

Приведем все сочетания из 2 элементов множества 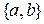по 3.

С повторениями: .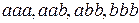

4. Математическое представление выборок. Размещение из n элементов по m – это просто последовательность длины m элементов из n -множества.

Сочетание без повторений из n элементов по m – это просто подмножество n -множества, содержащее ровно m элементов.

Сочетание с повторениями из n элементов по m – это график некоторого отображения a из множества первых m натуральных чисел в заданное n -множество: 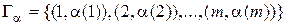. Только сочетание мы записываем мы проще: a₁a₂…a _m.