Растяжении, сжатии

Статически неопределимые задачи при центральном

К статически неопределимым относятся конструкции, в которых число неизвестных усилий превышает количество уравнений равновесия. На рис.3.7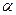представлена статически опреде-

лимая система: она имеет три неизвестных реакции и три уравнения статики. На рис.3.7 b изображена система, у которой четыре неизвестных усилия N_1, N₂, H,V, а уравнений равновесия у неё также три, следовательно, эта система будет один раз статически неопределимой.

Для определения внутренних усилий N_1, N₂ воспользуемся уравнением равновесия

∑М₀ =0, N₁∙ b+ N₂∙ с - F∙α=0 (3.1). Дополнительное уравнение можно получить, рассмотрев перемещения совместно деформируемых стержней (уравнение совместности деформаций). Считая горизонтальный стержень абсолютно жестким (недеформируемым), получим (рис.3.8)

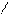
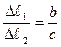, так как 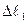=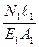, 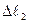=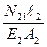, то 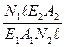= 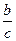. Выразим из этого уравнения усилие первого стержня 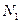=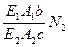и подставим его значение в уравнение равновесия (3.1).

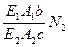b + N₂ c = F α, откуда следует , .

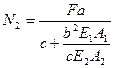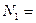
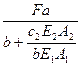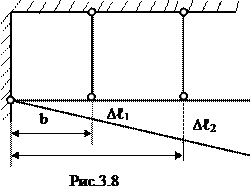Из полученных значений N₁ и N₂ следует, что статическая неопределимость конструкций может быть раскрыта, если известны жесткости её элементов. Так как с увеличением жесткости первого элемента Е₁А₁ усилие N₁ возрастает, а N₂ уменьшается и наоборот, то в статически неопределимых конструкциях полного использования прочностных свойств материала невозможно.

Рассмотрим случай, когда элементы конструкции выполнены из одного материала, т.е., Е₁=Е₂=Е, [σ]₁=[σ]₂=[σ], а также примем, что площади стержней и их длины одинаковы. А₁=А₂=А, ℓ₁ =ℓ₂ =ℓ, тогда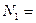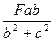, , 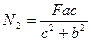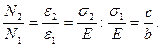Из последнего соотношения следует, что σ₂ > σ₁ в 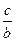раз, поэтому σ_наиб =σ₂ =[σ], σ₁ < [σ].