По найденным координатамотметим на чертеже сечения его центр тяжести с, проведём через него центральные оси х,у, параллельные центральным осям элементов, и вычислим относительно их моменты инерции, используя формулы преобразования моментов инерции при параллельном переносе осей, одни из которых центральные:
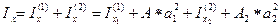 ;
;
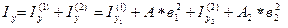 ;
;
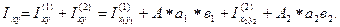
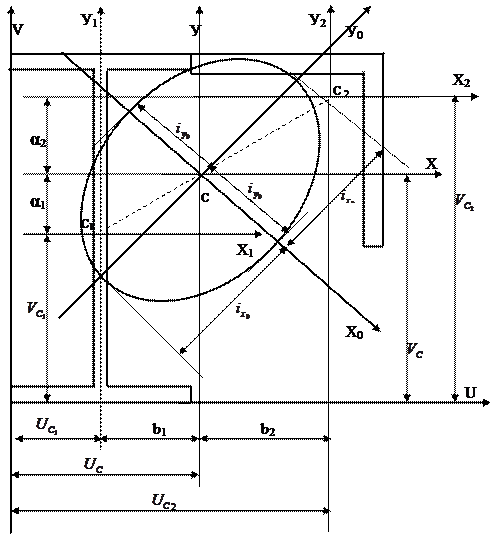 |
Здесь: a 1, в 1 –расстояния между центральной осью сечения х центральными осями элементов сечения х1 и х2;
a 2, в 2 - – расстояния между центральной осью сечения у и центральными осями элементов сечения у1 и у2.
|
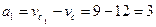 см,
см, 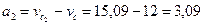 см,
см, 
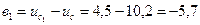 см,
см, 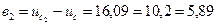 см.
см.
Осевые моменты инерции первого элемента (двутавра) относительно собственных центральных осей x1,y1: 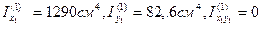
Осевые моменты инерции второго элемента (уголка) относительно собственных центральных осей х2,у2: 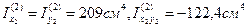 .
.
С учетом записанных формул и значений моментов инерции относительно собственных центральных осей получим:
Iх=1290+23,4*(-3)2+209+22,8*(3,09)2=1927,3 см4,
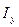 =82,6+23,4*(-5,7)2+209=22,8*(5,89)2=1804,9 см4,
=82,6+23,4*(-5,7)2+209=22,8*(5,89)2=1804,9 см4,
Iху=0+23,4*(-3)*(-5,7)-122,4+22,8*3,09*5,89=692,7 см4.
 2014-02-02
2014-02-02 994
994








