Внутренние усилия при изгибе

Рассмотрим в условиях статического равновесия балку, нагруженную сосредоточенной силой F, распределенной нагрузкой с интенсивностью q=q(z) и парой сил m (рис.6.7 а). Применяя метод сечений, разделим брус мысленно на две части (рис. 6.7 в). Для того чтобы каждая из частей находилась в равновесии, в сечении необходимо приложить поперечную силу Q и изгибающий момент М (рис.6.7 с ). Эти силовые факторы определяются из уравнений равновесия одной из частей бруса по следующим правилам: поперечная сила Q в каком либо

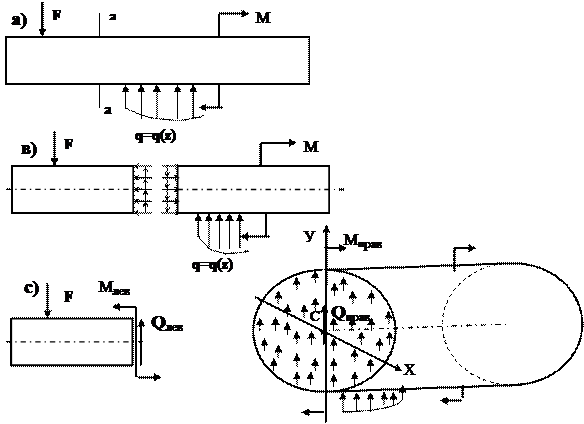
сечении балки равна сумме проекций всех внешних сил, расположенных по одну сторону от сечения, на направление перпендикулярное оси балки; изгибающий момент М в каком либо сечении балки равен сумме моментов всех внешних сил, расположенных по одну сторону от сечения относительно центра тяжести этого сечения.

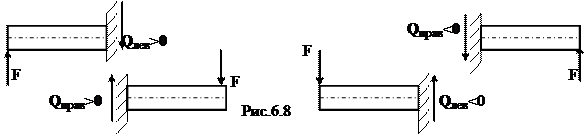
Правила знаков при определении поперечной силы: поперечная сила Q считается положительной, если внешняя сила стремится повернуть рассматриваемую часть балки отно-сительно сечения по часовой стрелке, если внешняя сила стремится повернуть рассматрива-емую часть балки против часовой стрелки, то Q принимается отрицательной. Эти правила знаков можно представить схемой (рис.6.8)

Правила знаков при определении изгибающего момента: если внешние силы изги-бают балку выпуклостью вниз, то изгибающий момент считается положительным, если выпуклостью вверх - отрицательным (рис. 5.9).