Мода — наиболее типичное, чаще всего встречаемое значение признака. В случаях интервальных рядов с равными интервалами, модальным интервалом считается интервал с наибольшей частотой, а при неравных интервалах — интервал с наибольшей плотностью.
Пример 6.5. Вычисление моды вариационного интервального ряда
| Интервал | Частота |
| 70—80 | |
| 80—90 | |
| 90—100 | |
| 100—110 | |
| 110—120 |
Mo = 100 + 10 × (45 - 30) / ((45 - 30) + (45 - 13)) = 103,2.
Медиана — значение варьирующего признака, приходящееся на середину ранжированной совокупности. При исчислении медианы интервального ряда сначала находится интервал, содержащий медиану. Медианному интервалу соответствует первый из интервалов, для которых накопленная сумма частот превышает половину общей совокупности наблюдений.
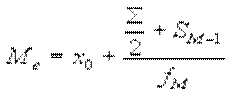 . (6.2).
. (6.2).
Внутри найденного интервала расчет медианы производится по формуле Ме = xl е, где второй множитель в правой части равенства показывает расположение медианы внутри медианного интервала, а х — длина этого интервала.
Медиана делит вариационный ряд пополам по частотам. Определяют еще квартили, которые делят вариационный ряд на 4 равновеликие по вероятности части, и децили, делящие ряд на 10 равновеликих частей.
· Что такое ряд распределения?
· Какие вы знаете виды рядов распределения?
· С какой целью ряды распределения изображают графически?
· Какие вы знаете графические изображения рядов распределения?
· Что собой представляют средние значения?
· Какие виды средних вы знаете?
· Какую роль играет однородность совокупности при выборе средней?
· Что такое структурные средние?
· Как строят кумуляту?
 2014-02-02
2014-02-02 935
935








