Ряды распределения и средние величины.
Рядом распределения называется упорядоченное распределение единиц совокупности на группы по какому-либо признаку. Виды рядов распределения:
· атрибутивный;
· вариационный;
· дискретный;
· интервальный.
Иными словами, ряд распределения — результат группировки. Под атрибутивным рядом понимается ряд распределения по атрибутивному признаку, не имеющему количественной меры. Например, атрибутивный ряд можно составить по признаку «Социальное положение», «Профессия», «Пол» и.т.д.
Пример 6.1. Атрибутивный ряд распределения
На предприятии провели группировку работников по признаку «Категория».
| Категория | Частота | Частость, % |
| Рабочие | 58,3 | |
| Служащие | 16,7 | |
| ИТР | 12,5 | |
| Прочие | 12,5 | |
| Итого | 100,0 |
Частота — количество элементов совокупности, которые имеют данное значение признака.
Частость — отношение частоты к общему количеству исследуемых элементов, т.е. объему совокупности. Частоту обозначим n, частость — р или j.
Пример 6.2. Пример дискретного ряда  .
.
Успеваемость в группе студентов-экономистов из 15 человек по одному из предметов.
| Оценки | Частота | Частость, % |
| 13,3 | ||
| 26,7 | ||
| 33,3 | ||
| 26,7 | ||
| Итого | 100,0 |
В интервальном ряду значение признака представляется в виде интервалов.
Пример 6.3. Пример интервального ряда
| Заработная плата, руб. | Частота | Частость, % |
| 100—200 | ||
| 200—300 | ||
| 300—400 | ||
| 400—500 | ||
| 500—600 | ||
| Итого |
Важно помнить: в интервальном ряду в качестве основного показателя интервала используется середина интервала х.
Для наглядного представления вариационных рядов используют графические методы: полигоны частот, гистограммы, кумулятивные кривые и т.п. Линейчатые и круговые диаграммы строятся для отображения структуры совокупности.
Наряду с диаграммами для наглядного представления распределения признака применяют такие линии, как полигон, кумулята, огива и др.
Полигон — ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси X откладываются значения признака, а по оси Y — частоты (рис. 6.1 ).
).
| Рис. 6.1. Полигон. |
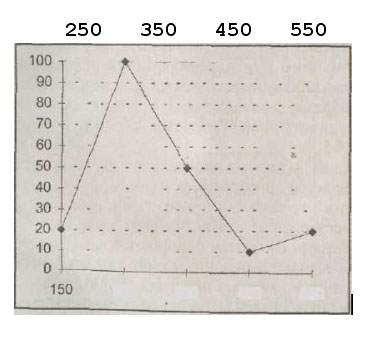 |
Гладкая кривая, соединяющая точки, — эмпирическая плотность распределения.
Кумулята — ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси X откладываются значения признака, а по оси Y — накопленные частоты (рис. 6.2 ).
).
| Рис. 6.2. Кумулята. |
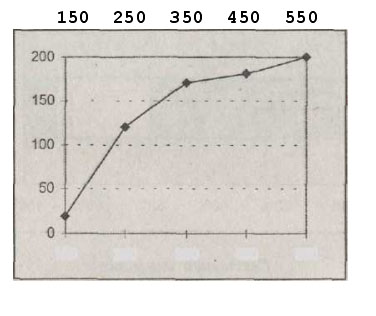 |
Для дискретных рядов на оси откладываются сами значения признака, а для интервальных — середины интервалов.
На основе гистограмм можно строить диаграммы накопленных частот с последующим построением интегральной эмпирической функции распределения.
 2014-02-02
2014-02-02 12036
12036
