На основе ФВЧ и ФНЧ типа “К” (LC) можно построить полосовые и режекторные фильтры.
1) Полосовые фильтры


Полосовые фильтры реализуют с помощью Т и П звеньев, при последовательном включении ФНЧ и ФВЧ. Такие фильтры не обеспечивают хороших характеристик, так как в полосе пропускания, вблизи ωс, входное сопротивление зависит от частоты, а в полосе задержания входное сопротивление реактивное, то есть нарушается условие согласования.
Чаще всего в качестве полосовых применяются фильтры на основе LC контуров.

У такого фильтра, при изменении частоты в сторону от резонансной, сопротивление последовательного звена возрастает, а параллельного падает. На резонансной частоте, входное сопротивление фильтров активное и равно Rн. На частотах ниже резонансной последовательный контур имеет – емкостной характер, а параллельного – индуктивный, то есть полосовой, фильтр превращается в ФВЧ типа “К”.
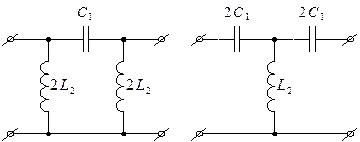
Частота среза ωс будет зависеть от С1 и L2:
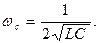
На частотах выше ωрез последовательный контур имеет индуктивный характер, а параллельного– емкостной характер т.е. полосовой фильтр превращается в фильтр типа “К”.
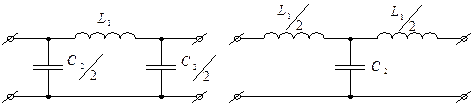
Частота среза ωс будет зависеть от L1 и С2:
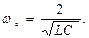
Если последовательный и параллельный контур имеют одинаковую ωс, то:
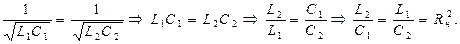
Тогда сохраняя эту пропорцию можно варьировать величинами C1L2=C2L1, то есть изменять частоты среза ФВЧ и ФНЧ в зависимости от того какая требуется полоса. В полосе пропускания входное сопротивление чисто активное, а вне полосы реактивное. На резонансной частоте ω0 входное сопротивление равно Rн.
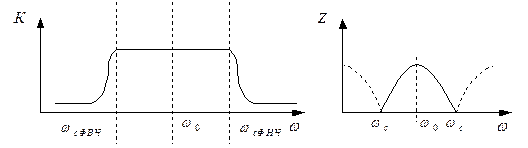
2) Заградительные фильтры.
Как и полосовые, выполняются на LC контурах, только последовательные и параллельные контура меняются местами.

На частотах ниже резонансной параллельный колебательный контур имеет индуктивный характер, а последовательный емкостное сопротивление т.е. полосовой фильтр превращается в ФНЧ.
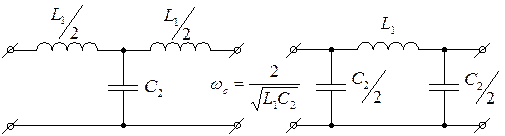
На частотах выше резонансной соответственно зверо полосового фильтра преобразуется в ФВЧ.
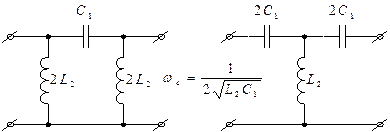

Частота среза ФНЧ 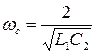 выбирается ниже, а частота среза ФВЧ
выбирается ниже, а частота среза ФВЧ 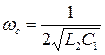 выше резонансной частоты параллельного и последовательного контуров.
выше резонансной частоты параллельного и последовательного контуров.
 2014-02-02
2014-02-02 7799
7799








