Ограничимся рассмотрением стационарного осесимметричного течения. Уравнения Навье—Стокса в этом случае имеет вид
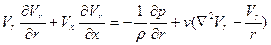 ;
;
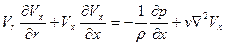 ; (2.141)
; (2.141)
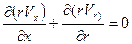
 |
где
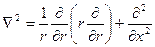 - оператор Лапласа в цилиндрической системе координат.
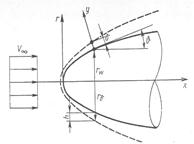
- оператор Лапласа в цилиндрической системе координат. Рис.2.7 Пограничный слой на теле вращения
При записи уравнений использована цилиндрическая система координат (r,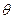 , х) (рис. 2.7), однако в силу осевой симметрии в уравнениях отсутствуют величины, зависящие от
, х) (рис. 2.7), однако в силу осевой симметрии в уравнениях отсутствуют величины, зависящие от 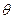 . Пусть уравнение поверхности обтекаемого тела есть r=rw(x), а внешняя граница пограничного слоя описывается уравнением
. Пусть уравнение поверхности обтекаемого тела есть r=rw(x), а внешняя граница пограничного слоя описывается уравнением 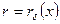 .
.
Разность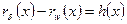 ,очевидно, будет мало отличаться от толщины пограничного слоя в сечении х, которая измеряется по нормали к образующей. Для внутренних точек пограничного слоя введем координату «у», отсчитываемую по нормали к поверхности
,очевидно, будет мало отличаться от толщины пограничного слоя в сечении х, которая измеряется по нормали к образующей. Для внутренних точек пограничного слоя введем координату «у», отсчитываемую по нормали к поверхности 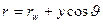 .
.
При x = const dr =dy, Vr=Vy. Поэтому дифференцирование по r можно заменить на дифференцирование по у. Кроме того, предположим, что 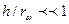 . В силу этого в уравнении неразрывности (третье уравнение системы (2.141) rможно заменить на rw и придать уравнению вид
. В силу этого в уравнении неразрывности (третье уравнение системы (2.141) rможно заменить на rw и придать уравнению вид
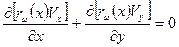 (2.142)
(2.142)
Если произвести оценку членов в первых двух уравнениях системы (2.141) тем же способом, что и в плоском случае, то получим уравнение пограничного слоя на теле вращения:
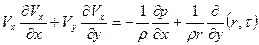
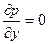 (2.143)
(2.143)
где обозначено r=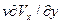 В системе (2.143) х является уже криволинейной координатой, отсчитываемой вдоль образующей от точки торможения. Однако вклад продольной кривизны в уравнения не учтен. Оценим погрешность, вносимую таким подходом. Пусть ускорение жидкой частицы в проекции на ось у равно ау. Очевидно, кривизна может дать вклад в это ускорение, равный (— Vx2/R), где R — радиус продольной кривизны. Порядок этой величины O(VX2/L). Следовательно, за счет кривизны будем иметь
В системе (2.143) х является уже криволинейной координатой, отсчитываемой вдоль образующей от точки торможения. Однако вклад продольной кривизны в уравнения не учтен. Оценим погрешность, вносимую таким подходом. Пусть ускорение жидкой частицы в проекции на ось у равно ау. Очевидно, кривизна может дать вклад в это ускорение, равный (— Vx2/R), где R — радиус продольной кривизны. Порядок этой величины O(VX2/L). Следовательно, за счет кривизны будем иметь
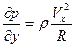
Остальные слагаемые в первом уравнении имеют меньший порядок О(Vx 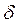 / L2). Введем средние значения скорости Vx ср и радиуса кривизны Rcp и проинтегрируем последнее уравнение
/ L2). Введем средние значения скорости Vx ср и радиуса кривизны Rcp и проинтегрируем последнее уравнение

Таким образом, вновь получаем, что если 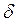 /Rcp <<1, то р(у) = const. Однако это условие может и не выполняться, особенно в кормовой части.
/Rcp <<1, то р(у) = const. Однако это условие может и не выполняться, особенно в кормовой части.
Влияние поперечной кривизны отражает последний член уравнения (2.143). Эта форма записи особенно важна для расчетов течения в кормовой области, где значения r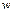 могут быть очень малыми и необходимо учитывать взаимовлияние жидких частиц, двигающихся в различных меридиональных плоскостях. Вообще говоря, если толщина пограничного слоя становится соизмеримой с радиусом образующей, нужно использовать теорию толстого пограничного слоя, отличительной чертой которого является зависимость давления от радиуса. Однако эта теория сложна и пока не получила применения в инженерной практике.
могут быть очень малыми и необходимо учитывать взаимовлияние жидких частиц, двигающихся в различных меридиональных плоскостях. Вообще говоря, если толщина пограничного слоя становится соизмеримой с радиусом образующей, нужно использовать теорию толстого пограничного слоя, отличительной чертой которого является зависимость давления от радиуса. Однако эта теория сложна и пока не получила применения в инженерной практике.
В классической постановке уравнение (2.143) записывается в более простой форме. Полагая r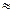 r
r , получим
, получим
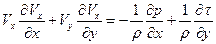
т. е. обычную форму записи плоского пограничного слоя. Однако уравнение неразрывности сохраняет прежний вид (2.142).
Получим теперь интегральное соотношение импульсов осесимметричного пограничного слоя. Перепишем уравнение выше в виде

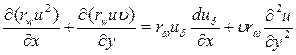
а уравнению (2.142) придадим вид
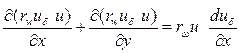
Для удобства здесь обозначено Vx=u, Vy= 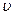 . Вычитая из обеих частей последнего уравнения левую и правую часть предыдущего, найдем
. Вычитая из обеих частей последнего уравнения левую и правую часть предыдущего, найдем
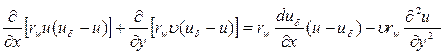
Интегрирование данного соотношения по y дает
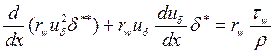
или
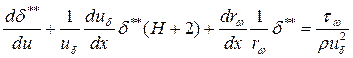
Здесь 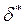 и
и 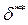 - толщина вытеснения и толщина потери импульса, вычисленные тем же способом, что и для плоского пограничного слоя.
- толщина вытеснения и толщина потери импульса, вычисленные тем же способом, что и для плоского пограничного слоя.
Если за основу взять систему (2.142), (2.143), то получим следующее интегральное соотношение импульсов:

или
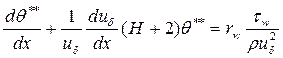
где 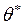 ,
, 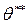 - площадь вытеснения и площадь потери импульса соответственно:
- площадь вытеснения и площадь потери импульса соответственно:
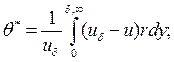
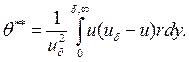
 2014-02-02
2014-02-02 836
836







