Математическая модель турбулентных течений жидкости

Уравнение Навье—Стокса как уравнение переноса завихренности.

Применим к уравнению (2.113) операцию rot. Это даст уравнение переноса вектора вихря скорости

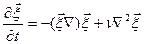. (2.117)

Как видим, процесс изменения завихренности со временем управляется двумя физическими процессами: конвекцией и диффузией.

При некоторых условиях упорядоченное слоистое ламинарное течение жидкости существенно меняет свой характер. Движение жидких частиц становится иррегулярным, хаотичным. Жидкие частицы помимо основного «переносного» движения вдоль общего направления потока совершают дополнительные колебания в продольном и поперечном направлениях. Полностью развитое такое хаотичное движение жидкости называют турбулентным.

Наступление турбулентного режима течения зависит от нескольких факторов. Однако главным из них является число Рейнольдса, представляющее собой отношение сил инерции к силам вязкого трения:

Re = .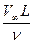

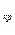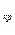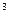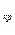При малых числах Re течение воды ламинарное, при некотором критическом значении Re ламинарный режим течения нарушается и при Re>Re течение становится турбулентным. Переходный режим осуществляется в действительности в некотором диапазоне чисел Рейнольдса 10< Re <10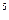в зависимости от условий течения, например от того, является ли рассматриваемая задача внутренней (течение в трубопроводах) или внешней (обтекание тел).

Не вдаваясь в детальный анализ условий перехода от ламинарного режима течения к турбулентному, сосредоточим внимание на возможностях математического описания развитого турбулентного течения.

Существует две точки зрения на эту проблему. Согласно первой из них, базирующейся на основополагающих идеях Рейнольдса, за основу можно принять уравнения Навье-Стокса, видоизменив их соответствующим образом и дополнив недостающими соотношениями в случае турбулентного движения. Эта точка зрения является доминирующей и благодаря ей к настоящему времени создан математический аппарат, позволяющий анализировать турбулентные течения в инженерных приложениях.

Вторая точка зрения заключается в том, что турбулентное движение является вероятностным процессом, а, следовательно, и уравнения, описывающие его, должны составляться на статической основе. Эта, в общем, правдоподобная идея, к сожалению, пока не привела к каким-либо существенным практическим успехам. Исследования в данном направлении продолжаются.