Приложение теоремы Лагалли.
Теорема Лагалли обладает замечательным свойством, поскольку позволяет анализировать силы и моменты в пространственных течениях. Правда, при этом возможности ограничены условиями применения метода особенностей.
Объясним парадокс Даламбера с точки зрения теоремы Лагалли. Для этого рассмотрим тело в равномерном потоке. Равномерный поток можно рассматривать как поток от источника, расположенного на 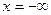 , и стока равной мощности, расположенного на
, и стока равной мощности, расположенного на 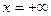 . Таким образом, тело будет испытывать равное по величине и противоположное по направлению силовое воздействие от источника и стока, т. е. суммарная сила будет равна нулю.
. Таким образом, тело будет испытывать равное по величине и противоположное по направлению силовое воздействие от источника и стока, т. е. суммарная сила будет равна нулю.
Другой подход к объяснению парадокса Даламбера состоит в следующем. Обтекание тела можно моделировать совокупностью источников и стоков, расположенных внутри тела. При этом суммарная мощность источников и стоков у тела с непроницаемыми стенками и постоянным объемом должна быть равна нулю. Но это сразу приводит к заключению, что
 .
.
Парадокс нарушается, если тело находится в канале переменного сечения, скорость на оси которого постоянна по времени, но переменна вдоль оси. Тогда скорости в точках, где находятся источники и стоки, будут различными, а, следовательно, суммарная сила будет не равна нулю.
Парадокс нарушается и при обтекании тела в окрестности твердой стенки (дна). Наличие твердой стенки можно смоделировать отображением соответствующих особенностей. Например, если в окрестности твердой стенки находится источник, то при отображении симметрично ему будет расположен источник с другой стороны стенки. По теореме Лагалли эти источники будут притягиваться друг к другу. Соответственно тело, генерируемое источниками и стоками, в окрестности твердой стенки будет испытывать силу, направленную к стенке.
Существуют обобщения теоремы Лагалли на случай нестационарных движений тела жидкости. Однако, этот случай будет проанализирован в гл. IV другим методом, а именно методом присоединённых масс.
В вязкой жидкости в отличие от идеальной касательные напряжения  при
при 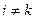 отличны от нуля. Таким образом, тензор напряжений элементарной жидкой частицы имеет общий вид:
отличны от нуля. Таким образом, тензор напряжений элементарной жидкой частицы имеет общий вид:
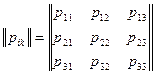 . (2.102)
. (2.102)
Для установления конкретного вида выражений  при
при 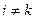 полезно обратиться к двухмерному слоистому течению, рассмотренному еще Ньютоном:
полезно обратиться к двухмерному слоистому течению, рассмотренному еще Ньютоном:
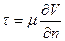 . (2.103)
. (2.103)
В общем случае пространственного движения вязкой жидкости
формулируется обобщенный закон Ньютона, устанавливающий линейную связь между тензором напряжений  и тензором скоростей деформации
и тензором скоростей деформации 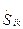 :
:
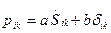 , (2.104)
, (2.104)
где 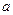 и
и 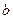 — некоторые скаляры;
— некоторые скаляры; 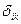 — символ Кронекера.
— символ Кронекера.
Примем дополнительную гипотезу, что
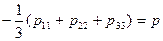 , (2.105)
, (2.105)
где р — давление. Таким образом, в вязкой жидкости давление в данной точке есть среднее арифметическое трех нормальных напряжений, приложенных к трем взаимно перпендикулярным площадкам в данной точке среды. Справедливость сделанной гипотезы подтверждается практикой.
Итак, в ньютоновской вязкой несжимаемой жидкости справедлив обобщенный закон (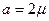 ,
,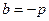 )
)
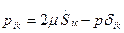 (2.106)
(2.106)
или в развернутой форме
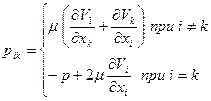
Уравнению сохранения количества движения (2.71) теперь можно придать более детализованный вид:
 . (2.107)
. (2.107)
При условии отсутствия разрывов возможно записать дифференциальную форму закона сохранения количества движения:
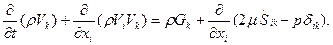 (2.108)
(2.108)
Заметим, что процессы в капельной жидкости протекают практически при постоянной температуре. Поэтому коэффициент динамической вязкости можно вынести из-под знака дифференцирования. Как и ранее, продифференцируем в левой части произведения, стоящие в скобках, и используем дифференциальную форму уравнения сохранения массы. В итоге найдем
 . (2.109)
. (2.109)
Здесь учтено, что
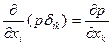 ,
,
так как 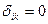 при
при 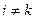 ,
, 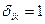 при i = k.
при i = k.
Рассмотрим последний член в правой части (2.109). Положим k = 1. Тогда в развернутом виде будет (множитель 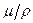 пока опустим):
пока опустим):
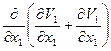 +
+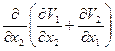 +
+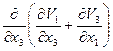 =
=
= 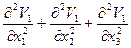 +
+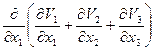 =
=
=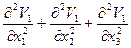 =
=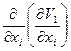 .
.
С учетом проделанных выкладок, а также путем введения коэффициента кинематической вязкости 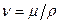 запишем окончательный вид уравнения (2.109):
запишем окончательный вид уравнения (2.109):
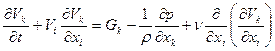 (2.110)
(2.110)
или в векторной форме:
 . (2.111)
. (2.111)
Уравнения (2.109), (2.110), (2.111) называются обычно уравнениями Навье - Стокса.
Если к системе (2.110) добавить уравнение неразрывности
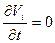 или div V =0, (2.112)
или div V =0, (2.112)
то получим систему из четырех уравнений для нахождения четырех скалярных функций 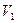 ,
, 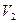 ,
, 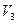 ,
, 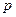 . Таким образом, система замкнута! Векторному уравнению (2.111) можно придать иную форму, напоминающую уравнение Громеки — Лэмба:
. Таким образом, система замкнута! Векторному уравнению (2.111) можно придать иную форму, напоминающую уравнение Громеки — Лэмба:
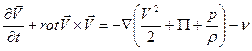 rot rot
rot rot 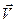 , (2.113)
, (2.113)
но содержащее дополнительное слагаемое, отражающее влияние вязкости. Сформированная математическая модель отражает слоистые упорядоченные течения жидкости, которые называются ламинарными.
Граничным условием на неподвижных твердых стенках теперь является требование обращения в нуль полной скорости
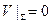 , (2.114)
, (2.114)
которое носит название условия прилипания.
На свободной поверхности кинематическое условие будет иметь вид:
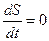 .
.
Динамическое условие даст два уравнения на свободной поверхности:
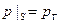 при i = k; (2.115)
при i = k; (2.115)
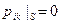 при
при 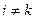 . (2.116)
. (2.116)
В качестве начальных условий задается граница области, занимаемая жидкостью, и поле скоростей в начальный момент времени.
 2014-02-02
2014-02-02 1590
1590
