Кинетическая энергия твердого тела.
Кинетическая энергия твердого тела равна
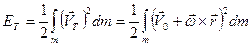 (4.2)
(4.2)
Это выражение можно заменить следующим:
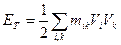 ,
,  , (4.3)
, (4.3)
где 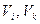 – компоненты скоростей тела;
– компоненты скоростей тела; 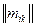 – матрица, характеризующая инерционные свойства тела.
– матрица, характеризующая инерционные свойства тела.
Запишем кинетическую энергию жидкости в виде

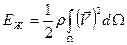 ,
,
или для случая потенциального течения
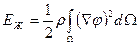 .
.
Имея в виду первую формулу Грина, получим:
 (4.4)
(4.4)
Таким образом, нахождение значения кинетической энергии вызванного течения жидкости свелось к вычислению интеграла по поверхности, ограничивающей жидкость. Причём подынтегральная часть содержит значения потенциала и его производной по нормали к поверхности.
Жидкость может быть ограничена поверхностью движущегося тела 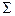 , неподвижными твердыми стенками (например, дном), свободной границей и, кроме того, должна существовать внешняя поверхность, расположенная на бесконечном удалении.
, неподвижными твердыми стенками (например, дном), свободной границей и, кроме того, должна существовать внешняя поверхность, расположенная на бесконечном удалении.
Ограничимся сначала рассмотрением случая движения тела в безграничной жидкости. В уравнении (4.1) тогда пропадет слагаемое, содержащее производную по обобщенной координате. Поверхность 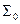 , ограничивающая жидкость, будет состоять из поверхности тела
, ограничивающая жидкость, будет состоять из поверхности тела 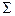 и поверхности сферы бесконечно большого радиуса
и поверхности сферы бесконечно большого радиуса 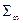 :
: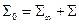
Оценим значение кинетической энергии жидкости на поверхности 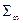 .
.
В пространственных течениях согласно поведению потенциала в пространстве произведение 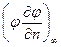 будет убывать как
будет убывать как 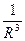 . Площадь же сферы растет пропорционально
. Площадь же сферы растет пропорционально 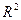 . Таким образом, кинетическая энергия на бесконечном удалении будет стремиться к нулю.
. Таким образом, кинетическая энергия на бесконечном удалении будет стремиться к нулю.
В плоских течениях произведение 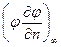 будет изменяться как
будет изменяться как  , а площадь цилиндрической поверхности будет расти пропорционально
, а площадь цилиндрической поверхности будет расти пропорционально 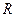 . Таким образом, кинетическая энергия жидкости в этом случае будет стремиться к бесконечности. Затруднение устраняется, если потребовать, чтобы источниковый член отсутствовал, и течение на бесконечности описывалось диполем. Отсутствовать должен и член, описывающий течение от вихря, так как при
. Таким образом, кинетическая энергия жидкости в этом случае будет стремиться к бесконечности. Затруднение устраняется, если потребовать, чтобы источниковый член отсутствовал, и течение на бесконечности описывалось диполем. Отсутствовать должен и член, описывающий течение от вихря, так как при 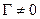 на бесконечности величина
на бесконечности величина  не исчезает.
не исчезает.
Таким образом, будем считать, что течение обладает однозначным потенциалом, исчезающим на бесконечности, так что 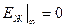 . Поэтому
. Поэтому
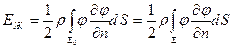
 2014-02-02
2014-02-02 592
592








