2014-02-02
520
Можно рассматривать твердое тело и жидкость как единую механическую систему, обладающую шестью степенями свободы. Кинетическая энергия этой системы будет слагаться из кинетической энергии твердого тела и кинетической энергии жидкости, соответствующей вызванному течению под влиянием движения тела. При таком подходе появляется возможность записи уравнений движения механической системы в виде уравнений Лагранжа второго рода:
, 
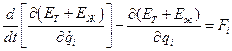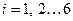(4.1)
где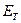 
– кинетическая энергия твердого тела; 
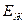– кинетическая энергия жидкости; 
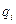– обобщенные координаты; 
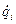– обобщенные скорости; 
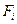– обобщенные силы.
Как известно, инерционные свойства тела характеризуются значениями массы, статического, центробежного и осевого моментов инерции. По смыслу сформулированного подхода к инерционным характеристикам твердого тела присоединяются соответствующие инерционные характеристики жидкости. В целях простоты различные типы инерционных свойств жидкости называют обобщенными присоединенными массами или просто присоединенными массами. Вследствие сказанного весь метод рассмотрения единой механической системы «тело — жидкость» получил название метода присоединенных масс.
|
|
|
Рассмотрим отдельные составляющие уравнения механической системы.
