Свойство симметрии присоединенных масс.
Прежде всего отметим свойство симметрии величин 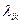 , которое вытекает из теоремы взаимности:
, которое вытекает из теоремы взаимности:
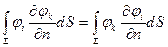 ,
,
т.е. 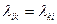
Это обстоятельство сразу снижает число неизвестных величин 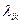 . Их вместо 36 остаётся только 21.
. Их вместо 36 остаётся только 21.
Кинетическую энергию жидкости можно представить в виде суммы трех частей, каждая из которых выражает энергию определенного вида движения:
1) кинетическая энергия поступательного движения
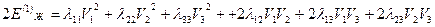 (4.9)
(4.9)
2) кинетическая энергия вращательного движения
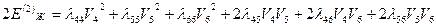 (4.10)
(4.10)
3) кинетическая энергия смешанного движения
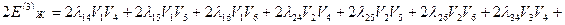
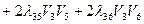 (4.11)
(4.11)
Нетрудно видеть, что в каждой части кинетической энергии присоединенные массы имеют свою размерность, характерную для рассматриваемого вида движения.
При поступательном движении 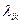 имеют размерность массы. Иными словами,
имеют размерность массы. Иными словами,
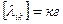 , при
, при 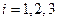 и
и 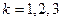
При вращательном движении 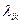 имеют размерность моментов инерции, т. е.
имеют размерность моментов инерции, т. е.
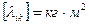 , при
, при 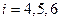 и
и 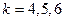
При смешанном движении 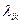 имеют размерность статических моментов. Иными словами,
имеют размерность статических моментов. Иными словами,
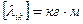 , при
, при 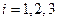 и
и 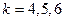
Таким образом, термином «присоединенные массы» обобщенно определены различные виды инерционных характеристик жидкости: масса, статические моменты и моменты инерции.
Инерционные свойства жидкости существенно отличаются от инерционных характеристик твердого тела. Достаточно сказать, что понятие массы у твердого тела является инвариантным для любого направления поступательного движения. В противоположность этому у жидкости при поступательном движении величины присоединённых масс зависят от направления движения. В общем случае
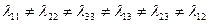
 2014-02-02
2014-02-02 762
762








