Крылья малого удлинения

В этом случае 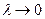, взаимодействие течения в смежных по потоку поперечных сечениях невелико и можно применить теорию тонкого тела. Ограничимся рассмотре­нием простейшего случая, а именно: обтекания плоского крыла (пластины) произвольной формы в плане, но с заостренной носо­вой частью (рис. 5.20).

Заменим пластину непрерывным вихревым слоем интенсивности 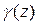(рис. 5.20).

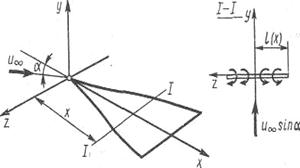
Рис.5.20 Схема крыла малого удлинения

Тогда возмущенная скорость в любой точке пластины будет

(5.15)

Если воспользоваться условием непротекания, получим интегральное уравнение для нахождения неиз­вестной функции 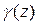, но в данном случае нам нужно построить решение первого типа, обращающееся в бесконечность на обоих концах интервала. После определения 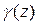перейдем к вычислению нагрузок, отсюда получим формулу Джонса:

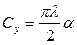(5.16)

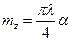(5.17)

Определим индуктивное сопротивление:

(5.18)

Переходя к безразмерным коэффициентам сил, записываем

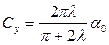(5.19)

На участках крыла, где размах остается неизменным, подъемная сила отсутствует. Подъемная сила возникает лишь на участке крыла с монотонно увеличивающимся размахом до его максимального значения. Суммарная подъемная сила определяется именно зна­чением максимального размаха крыла.

Пределы применимости изложенной теории можно приближенно оценить путем сравнения с экспериментальными результатами или расчетными данными, полученными по более строгим теориям. Для этой цели на рис. 5.21 приведены экспериментальные результаты и расчетные данные, полученные по теории несущей поверхности и теории тонкого тела для прямоугольных и стреловидных крыльев.

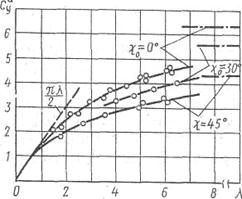
Рис.5.21

Сравнение показывает, что прибли­женная формула Джонса дает удовлетворительные результаты до удлинений порядка единицы.