Вязкостное сопротивление тел вращения и несущих поверхностей

Течение жидкости около пространственных тел характеризуется непостоянством давления на их поверхности. Если подходить к анализу таких течений с позиций теории пограничного слоя, то это означает, что в отличие от обтекания пластины необходимо принимать во внимание дополнительный размерный параметр — градиент давления. Течения такого типа называются градиентными. Для качественной оценки влияния этого параметра на характеристики течения в пограничном слое рассмотрим дифференциальное уравнение количества движения:

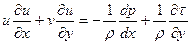применимое и для ламинарного, и для турбулентного режимов течения.

На твердой стенке (у=0) должно выполняться условие прилипания u=v=0. Поэтому

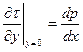(6.22)

Полученное соотношение сразу позволяет дать оценку изменения τ в фиксированных сечениях х. Дополнительным соображением может служить также очевидное условие равенства нулю касательного напряжения на внешней границе пограничного слоя. Если dp/dx<0 (течение в носовой части), то 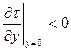, т.е. касательное напряжение падает с увеличением расстояния от стенки (рис. 6.6,a)

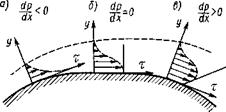Рис. 6.5 Изменение τ в фиксированных сечениях х.

Если dp/dx=0 (продольное обтекание пластин или цилиндра), то 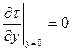. Это означает, что в непосредственной окрестности стенки касательное напряжение постоянно, а затем падает до нуля (рис. 6.5, б). Наконец, если dp/dx>0 (течение в кормовой части тела), то 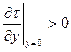, т.е. при удалении от стенки касательное напряжение вначале растёт. Но по условию, на внешней границе пограничного слоя оно должно обратиться в ноль. Следовательно, эпюра τ(y) должна иметь максимум (рис.6.5, в).

При ламинарном течении, согласно закону вязкого трения Ньютона,

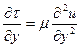
Следовательно, можно записать в соответствии с (6.22)

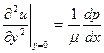
Таким образом можно сделать некоторые заключения и о профиле скорости u(y) в сечениях пограничного слоя. Если dp/dx<0, то 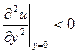. Это означает, что кривая u(y) в точке y=0 обращена выпуклостью вниз (рис.6.6,а). Если dp/dx=0, то 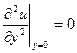, т.е. в окрестности стенки профиль скорости представляет собой прямую линию (кривизна равна нулю). Это заключение полностью соответствует введенному ранее понятию вязкого подслоя с линейным профилем скорости u⁺=у⁺ (рис. 6.6, б). Наконец, если dр/dх>0, то и 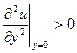, т. е. кривизна профиля u(у) в точке у=0 направлена вверх. Но на внешней границе пограничного слоя профиль u(у) всегда обращен выпуклостью вниз. Отсюда следует вывод, что в этом случае профиль u(у) должен иметь точку перегиба (точка А на рис. 6.6, в).

Воспользуемся гипотезой Буссинеска об эффективной вязкости турбулентного течения и запишем выражение для трения на стенке в одинаковой форме для ламинарного и турбулентного режимов течения:

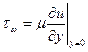
Нетрудно видеть, что при 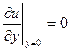в нуль обратится и τ_ω (рис.6. 7, а). Сечение, в котором будет наблюдаться это явление, будет сечением отрыва пограничного слоя. В самом деле при 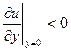соответственно будет и τ_ω <0. В пограничном слое возникнет возвратное течение (рис. 6. 7, б). Пунктирная линия соответствует линии нулевых скоростей.

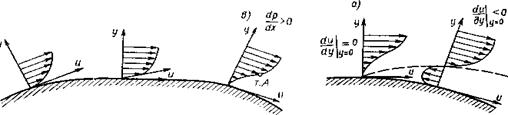Рис. 6.6 Изменение р на поверхности Рис. 6.7 Изменение u на поверхности

Из предыдущего ясно, что при dр/dx<0 профиль u(у) всегда выпуклый вниз. Следовательно, перегиб профиля может произойти только в условиях нарастания давления dр/dx >0. Возникновение точки перегиба приводит к потере устойчивости ламинарного течения, а в дальнейшем при определенных условиях и к отрыву пограничного слоя. Наблюдениями установлено, что сечение перехода ламинарного пограничного слоя в турбулентный примерно совпадает с сечением минимального давления. Отсюда становится понятной важность понимания воздействия градиента давления на характеристики пограничного слоя вдоль по потоку.

Степень воздействия градиента давления на структуру турбулентного пограничного слоя удобно оценивать с помощью метода размерностей. В безградиентном пограничном слое существуют два линейных масштаба: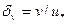— внутренний (вязкий) масштаб и δ — толщина пограничного слоя — внешний масштаб.

В градиентном течении можно ввести дополнительный линейный масштаб: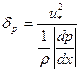-масштаб градиента давления. Степень воздействия градиента давления на течение в различных областях турбулентного пограничного слоя будет определяться соотношением масштаба δ_р с масштабами δ_V и δ. При dр/dх = 0 имеем 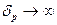. С ростом градиента давления масштаб δ_р уменьшается, приближаясь к значениям δ и далее к δ_v. Таким образом, градиент давления относится к числу внешних воздействий на пограничный слой. В случае 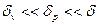градиент давления оказывает воздействие частично на турбулентное ядро потока (логарифмический закон) и на внешнюю область (закон дефекта скорости и следа). Вязкий подслой и буферная зона почти «не чувствуют» присутствия градиента давления. В случае, когда δ_p~δ_v, градиент давления сказывается и на течении в непосредственно пристеночной области, в вязком подслое и в буферной зоне. Дальнейшие конкретные заключения нужно делать уже с учетом знака dр/dх. Если dр/dх<0, то при 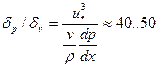начинается реламинаризация пограничного слоя или иначе говоря, обратный переход турбулентного пограничного слоя в ламинарный. Если же dр/dх>0, то при δ_p/ δ_v=50 наблюдается интенсификация «взрывных процессов» в вязком подслое, появление «местных отрывов». Устанавливается режим перемежающегося отрыва, который переходит затем в развитый отрыв. Другими словами, значение δp/ δv=50 приближенно характеризует переход к предотрывному режиму течения.