Вязкостное сопротивление тел простейшей формы

Современное состояние теории вязких течений не позволяет аналитическим и расчетным путем предсказывать сопротивление сложных конфигу­раций особенно при наличии отрывных зон. Поэтому важную роль играют экспериментальные методы, а в процессе проектирования необходимо уметь правильно использовать приближенные теоретические прогнозы и доступные экспериментальные данные. Ориентируясь на методологию эквивалентного тела, проектанту полезно знать гидродинамические характеристики простейших геометрических форм, часто встречающихся на практике. Часть этих характеристик приводится в данном разделе.

Остановимся прежде всего на продольном обтекании бесконеч­ного кругового цилиндра.

Это течение можно рассматривать как предельное течение около удобообтекаемого тела бесконечного удлинения. Так же, как и на пластине, в данном случае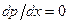. Однако сопротивление трения цилиндра может отличаться от сопротивления трения пластины. Причиной служит поперечная кривизна цилиндрической поверхности. При заданной скорости набегающего потока этот эффект будет проявляться по-разному не только в зависимости от Re_L, но и от 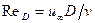, где D — диаметр цилиндра. При больших удлинениях (L/D>20) наблюдается заметное увеличение сопротивления. Ко­личественная оценка эффекта поперечной кривизны может быть вы­полнена либо по теоретической формуле

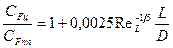
либо по эмпирическим зависимостям

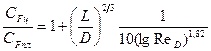
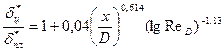
справедливым в диапазоне 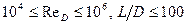. При умерен­ных удлинениях поправка на поперечную кривизну невелика.

Выразим коэффициент сопротивления тела вращения че­рез площадь сравнения :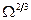

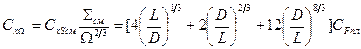(6.26)

Если тело вращения имеет донный срез, диаметр которого d_дон меньше диаметра миделя D, расчет выполняется по формуле

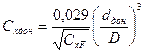
где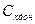и 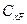вычисляются по площади миделя.

Гипотезу эквивалентной пластины логично распространить и на несущие поверхности (крылья, стабилизаторы, рули). Сопротивление крыла с телесным профилем будет отличаться от сопротивления пластины за счет увеличения средней скорости над крылом по срав­нению со скоростью набегающего потока, а также за счет появле­ния сопротивления формы. Введя поправочный коэффициент, вяз­костное сопротивление крыла с телесным профилем выразим через сопротивление пластины:

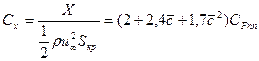(6.27)

где с - относительная толщина профиля; S_KP - площадь крыла в плане.

Обратим внимание на то, что свободный член в скобках равен 2. Это объясняется тем, что у крыла за площадь сравнения берется площадь в плане, а не вся омываемая площадь как у плас­тины. Формула (6.27) дает приемлемую точность до .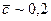

Поперечное обтекание пластин характеризуется развитым от­рывным течением в донной области. Надежные результаты по коэф­фициентам сопротивления достигаются в этом случае экспери­ментальным путем.