Позиционные силы и моменты корпуса

К категории позиционных относятся силы и моменты, действую­щие со стороны жидкости на тело при его неизменной ориентации (позиции) относительно стационарного набегающего потока. В пря­мом (не обращенном) движении сформулированным условиям со­ответствует равномерное чисто поступательное движение тела в жидкости. Для простоты ограничимся рассмотрением движения тела лишь в вертикальной плоскости. В дальнейшем будет рассмат­риваться лишь обращенное движение. В этом случае течение будет формироваться вектором скорости потока на бесконечности 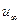, об­разующим с продольной осью тела угол атаки 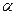, и конфигурацией обтекаемого тела. В целях наглядности будем считать тело осесимметричным и имеющим плавные обводы. Как обычно, обозначим максимальный диаметр тела через D, длину через L, а объем че­рез 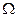. Ранее было показано, что в стационарном потенциальном пото­ке суммарная гидродинамическая сила равна нулю. На тело вра­щения действует лишь момент

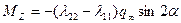
который является кабрирующим и способствует развороту тела поперек потока.

Отсутствие суммарной поперечной силы указывает на то, что момент М_Z появляется в следствии существования пары сил и не за­висит от выбора точки отсчета. В носовой области формируется подъемная сила, а в кормовой области создается сила обратного знака.

В вязкой жидкости картина течения существенно изменяется. Пограничный слой как бы деформирует реальные очертания тела, и наибо­лее заметно в кормовой области.

В качестве иллюстрации на рис. 6.8 показаны эпюры коэф­фициента давления 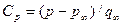в четырех поперечных сече­ниях тела вращения, контур которого показан внизу рисунка. В це­лях большей выразительности взят довольно большой угол атаки 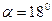. Число Рейнольдса 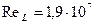. На рис. 6.8 сплошной линией и стрелками изображены расчетные эпюры, полученные по теории невязкой жидкости, точками отмечены опытные значения С_р

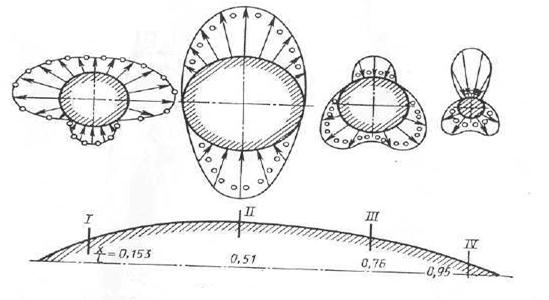
Рис. 6.8 эпюры коэф­фициента давления

В носовой области (сечения 1 и 2) наблюдается удовлетворительное совпаде­ние расчетных и экспериментальных значений. Поперечная сила создается не только за счет повышения давления с наветренной сто­роны корпуса, но и за счет разрежения с подветренной стороны. Последний фактор, пожалуй, даже преобладает. В кормовой обла­сти (сечения 3 и 4) реально измеренные поля давлений сущест­венно отличаются от расчетных. Отчетливо видно выравнивание полей давления в окружном направлении, что, естественно, должно приводить к падению величины нормальной силы.

К настоящему времени получены обширные сведения также и о суммарных силах и моментах на корпусах различной геометрии при круговой продувке, т. е. при углах атаки от 0 до 180°.

Расчет обтекания тела вращения вязким потоком, набегающим под углом атаки α, возможен к настоящему времени методами, ос­нованными на хорошо изученной теории идеальной жидкости, и ис­пользующими поправочные функции, коэффициенты эмпирического типа.

Наиболее простой и наглядной является гипотеза плоских сече­ний. В этом случае элементарная нормальная сила dY, приходящаяся на элементарный отрезок продольной оси dx, равна

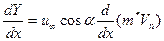(6.28)

где 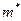- присоединенная масса поперечного сечения корпуса. В случае кругового сечения 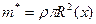; 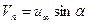- скорость, нормальная к оси х корпуса.

Если ось корпуса прямолинейна, т.е. 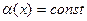, а следовательно, и .

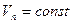В этом случае

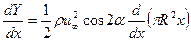
Ho 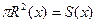есть площадь поперечного сечения. Поэтому можно также записать

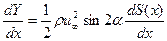
или

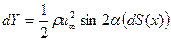
Если теперь выполнить интегрирование по всей длине корпуса от х=0 до x=L, то получим

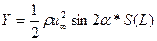
При S(L)=0 получим уже известный результат, что суммарная сила равна нулю. Однако если учесть высказанные ранее соображения о снижении или полном исчезновении несущих свойств корпуса в кормовой области в присутствии вязкости, то в первом приближении можно ограничиться рассмотрением течения в носовой домидельной области. Тогда

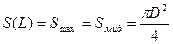
и

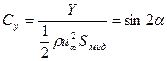
Вся теория справедлива при малых углах атаки. Поэтому

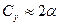(6.29)

Итак гипотеза плоских сечений, основанная на модели идеальной жидкости, дает количественный результат лишь с привлечением опытных наблюдений над течениями вязкой жидкости.

Аналогичным путем можно составить формулу и для расчета продольного момента

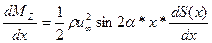(6.30)

Отсюда следует

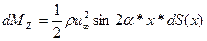
Проинтегрируем, это уравнение, применив в правой части ин­тегрирование по частям:

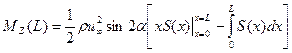
При x = 0, S(0) =0. Если допустить, что при x = L, S(L) =0, полу­чим

или так как 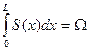- объем тела,

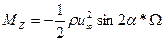(6.31)

Составим коэффициент продольного момента

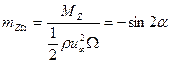
или

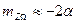(6.32)

Подмечено, что линейные теории дают удовлетворительные ре­зультаты по суммарным нагрузкам и гораздо худшие по распреде­ленным параметрам. В данном случае это относится к нахождению центра давления с помощью найденных значений M_z и С_y. Расхож­дения между теорией и экспериментами здесь довольно значительны.

Расчетные значения становятся точнее, если прибегнуть к тео­рии пограничного слоя и вместо реальной конфигурации R = R(x) рассматривать деформированную 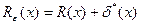, где 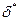- толщина вытеснения пограничного слоя.