Соотношения подобия

Скорость течения «u» жидкости с поли­мерными добавками в окрестности бесконечной пластины будет определяться следующими размерными параметрами растворите­ля: τ_0, ρ₀, μ₀, а также молекулярным весом М_*, длиной молекулы l и характерным временем взаимодействия t полимера, а также «плотностью полимера» ρ_р, под которой понимается отношение массы полимера к объему растворителя, и расстоянием от стенки у. Таким образом, имеем 9 размерных величин и согласно π-теореме можно составить 6 безразмерных комплексов. Укажем один из возможных вариантов записи закона течения в безразмерной форме:

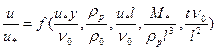(6.52)

Нетрудно видеть, что отношение плотностей чистой жидкости и полимера определяет концентрацию

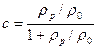(6.53)

Последние два безразмерных комплекса в (6.52) характеризуют данный полимер и не зависят от условий течения и характеристик раствора. Поэтому для выбранного полимера мож­но записать

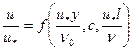(6.54)

Если рассматривать обтекание пластины конечной длины L по­током со скоростью u_∞, то в задаче появятся дополнительно две размерные величины и, следовательно, два дополнительных без­размерных комплекса:

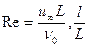
На значительном удалении от стенки, ближе к границе погра­ничного слоя δ, влияние добавок полимеров будет несуществен­ным и поле скоростей «u» будет определяться размерными пара­метрами u_δ, δ, τ_w, ρ₀, у. Это дает возможность сформировать за­кон дефекта скорости в общем виде:

(6.55)