Обтекание пластины при щелевой подаче полимера

Влияние шероховатости.

Рис. 6.13 Рис. 6.14

Шероховатость вносит в задачу новый линейный параметр — высоту бугорков шероховатости h, что при­водит к расслоению интегральных характеристик потока по без­размерной величине этого параметра Rе_h= u_∞h/υ₀. Соответствую­щие кривые С_F=f(Rе_L, Rе_h, с) приведены на рис. 6.14. Как ви­дим, при умеренных числах Рейнольдса кривые имеют характер­ную ложкообразную форму, а при больших числах Рейнольдса Rе_L кривые выходят на асимптотические значения, не зависящие от Rе_L и совпадающие с аналогичными значениями для чистой воды при той же шероховатости. Иными словами, при определен­ных значениях Rе_L шероховатость подавляет эффект снижения со­противления за счет полимерных добавок, и этот процесс насту­пает тем раньше, чем выше шероховатость. Объяснение этого факта состоит в том, что полимерные добавки перестраивают те­чение в узкой пристенной области (в области вязкого подслоя и буферной зоны). Пока бугорки шероховатости не выступают за пределы буферной зоны, эффект Томса действует. Если же шеро­ховатость слишком велика, так что бугорки выступают за преде­лы буферной зоны, устанавливается квадратичный закон сопро­тивления, как это имеет место и в течениях чистой жидкости.

Для прак­тических приложений более интересным и важным является слу­чай дискретной подачи полимерных растворов в пристенный по­ток. Подачу желательно производить в тангенциальном направле­нии. Устройство и интенсивность подачи не должны вносить су­щественных изменений в пограничный слой.

Экспериментами установлено, что за щелью подачи полимера на пластине устанавливается диффузионный слой, в котором мож­но выделить четыре зоны. Начальная зона 1 примыкает к источнику полимерного раствора. Диффузионный слой погружен в вязкий подслой. Протяженность зоны зависит от размеров источ­ника относительно толщины вязкого подслоя, скорости подачи полимера и величины молекулярной диффузии. В промежуточ­ной зоне 2 размер диффузионного слоя много больше, чем тол­щина вязкого подслоя, но он весь находится в пределах динамического пограничного слоя 6. Диффузия вещества высока и уста­навливается приблизительно подобный профиль концентрации:

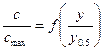
где 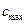— максимальная концентрация на стенке; у_0,5 — ордината, при которой с/с_mах=0,5.

Протяженность этой зоны — 20...40 толщин пограничного слоя в сечении подачи. Переходная зона 3 характеризуется дальнейшим ростом толщины диффузионного слоя, но с меньшей скоростью, так как его внешняя граница достигает области «зако­на следа» динамического пограничного слоя, где турбулентность ниже. Конечная зона 4 характеризуется полным развитием диффузионного слоя, совпадением границы последнего с границей динамического пограничного слоя. Максимальная концентрация наблюдается на стенке. Она убывает вниз по потоку по закону

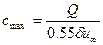(6.56)

где Q — объемный расход полимера на единицу ширины щели.

Схема течения изображена на рис. 5.15, где 5 и 6 — границы диффузионного и динамического пограничного слоев соответствен­но, 7 и 8 — профили концентрации и скорости. Обратим внимание на профиль концентрации. Он подобен как бы перевер­нутому профилю скорости. В окрестности стенки концентрация на большом участке по вертикали сохраняет почти постоянное значе­ние с_mах, а затем падает до нуля во внешней области погранично­го слоя. Но ранее было показано, что воздействие полимеров на поток сказывается, главным образом, в пристенной области (бу­ферном подслое). Следовательно, при построении приближенной методики расчета эффекта снижения сопротивления от линейного источника полимеров можно принять, что в каждом поперечном

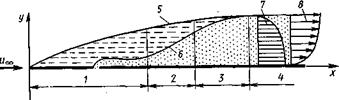
Рис. 5.15 Схема течения

сечении потока течение характеризуется постоянной концентра­цией с_mах, которая определяется формулой (6.56). Такое пред­положение позволяет избежать решения дифференциальных урав­нений диффузионного слоя, что существенно упрощает задачу.

В принятой постановке задача сводится к совместному решению уравнений динамического пограничного слоя и соотношения диффузии полимера (6.56). Будем считать, что сечение вдува совпадает с сечением перехода ламинарного пограничного слоя в турбулентный. Уравнение динамического пограничного слоя целесообразно использовать в форме, даваемой теоремой импульсов. Для подсчета интегральных параметров слоя применяется профиль скорости

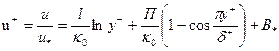(6.57)

где 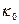=0.4 – постоянная Кармана; П =0.55 – параметр Коулса.

Величина В_* включает в себя поправку ΔВ на присутствие полимерных растворов:

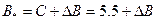(6. 58)

Наиболее просто поправка ΔВ вычисляется по формуле Майера:

(6.59)

где α_*= α_*(с,М_*) – множитель, учитывающий концентрацию и природу полимерного вещества. Коэффициент α_* вычисляется по формулам, аппроксимирующим экспериментальные данные, например

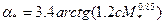(6.60)

Поправка Майера дает удовлетворительные результаты при малых величинах снижения сопротивления.

Более сложная модель расчета В_* предложена школой Л. И. Седова. На основании обработки данных многочисленных экспериментов в трубах получена следующая аппроксимирующая формула:

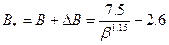(6.61)

где

, ; ;

; ;

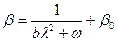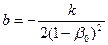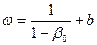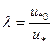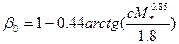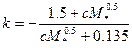
Систему определяющих уравнений пограничного слоя можно представить в следующем составе: уравнение импульсов, закон сопротивления, одномерное уравнение диффузии.