Частица, находящаяся в сдвиговом потоке, испытывает растягивающие усилия и вращательный момент. Молекулы полимеров обладают упругостью и при отсутствии внешних нагрузок сворачиваются в асимметричные клубки. Сдвиговый поток стремится развернуть этот клубок и сориентировать получающуюся линейчатую конфигурацию вдоль течения. После того, как это произойдет, полимеры начинают проявлять свойство снижения сопротивление. Ясно, что количественную оценку момента начала действия полимеров нужно производить с привлечением величины напряжения трения на стенке или эквивалентной ей величины динамической скорости 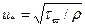 . Значение динамической скорости u*о, при которой начинается снижение сопротивления, называется пороговой (или начальной) динамической скоростью. На основании экспериментальных исследований получено следующее условие для вычисления пороговой динамической скорости:
. Значение динамической скорости u*о, при которой начинается снижение сопротивления, называется пороговой (или начальной) динамической скоростью. На основании экспериментальных исследований получено следующее условие для вычисления пороговой динамической скорости:
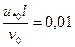 , (6.51)
, (6.51)
где 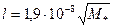 — линейный размер молекулы; М* — молекулярный вес полимера; v о — коэффициент кинематической вязкости растворителя.
— линейный размер молекулы; М* — молекулярный вес полимера; v о — коэффициент кинематической вязкости растворителя.
Как видим, пороговая динамическая скорость определяется только физическими свойствами полимера и не зависит от концентрации раствора, условий течения.
Существование пороговой динамической скорости заставляет определять границы применимости метода снижения сопротивления полимерными добавками. В самом деле при обтекании пластины динамическая скорость падает вдоль пластины по потоку. Значит, положительный эффект от полимерных добавок будет наблюдаться в том случае, если в начале турбулентного режима на пластине динамическая скорость будет превышать пороговую динамическую скорость. Это условие, как правило, выполняется. И кроме того, полимерные добавки будут снижать сопротивление лишь до сечения, где динамическая скорость сравняется с ее пороговым значением. Ниже от этого сечения по потоку снижения сопротивления не будет. Если при заданных условиях течения такое сечение на пластине конечной длины существует, то пластина называется короткой. В противоположном случае пластина называется длинной.
 2014-02-02
2014-02-02 788
788








