Проникание конуса

До конца удается решить задачу о погру­жении конуса. Если скорость погружения конуса постоянна (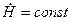), то задача является автомодельной, т. е. в переменных 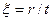и 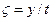геометрия ее течения остается неизменной. Аналогич­ное свойство сохраняется и в случае 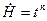. В силу автомодельност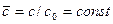и и 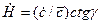. Тогда

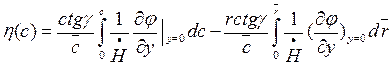
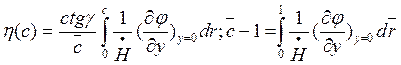(8.45)

Интегрирование дает

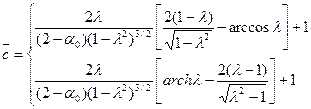
первое решение при 0<λ<1, второе при λ>1.

Как видим, коэффициент подпора воды зависит от угла заострения конуса (величины λ), причем таким образом, что при 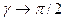(тупой конус) влияние угла наиболее значительно, а при оно исчезает.

Если в качестве эквивалентного тела принять диск (случай силь­но затупленных конусов), то коэффициент подпора становится не зависящим от угла заострения и равным . При 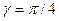экви­валентный эллипсоид вырождается в сферу и тогда .

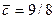Присоединенная масса эквивалентного эллипсоида вращения с учетом коэффициента подпора воды может быть выражена теперь через коэффициент

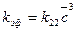(8.46)

Переходя к оценке силового взаимодействия погружающегося тела с жидкостью, нужно отметить, что в основе расчета силы со­противления лежит теорема о количестве движения, которую в рас­сматриваемом случае можно представить в виде

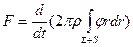(8.47)

где Σ — поверхность твердого тела, в конкретном примере - конуса; S — поверхность свободной поверхности.

Согласно принятому допущению, интегрирование по Σ приведет к понятию присоединенной массы эквивалентного эллипсоида, прин­цип нахождения которой приведен. Остается оценить влияние сво­бодной поверхности. Введем обозначение

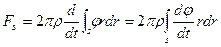(8.48)

С учетом того, что

; ;

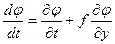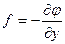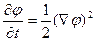
выражение для силы F_S приобретает вид

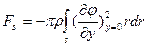(8.49)

Или

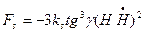(8.50)

где

(8.51)

Вычисление интегралов приводит к формулам

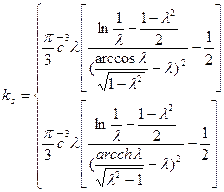
первое решение при 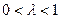, второе при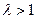

В случае эквивалентной сферы (λ=1)

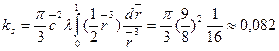(8.52)

В случае эквивалентного диска k_s = 0.

Запишем теперь выражение для эффективной присоединенной массы:

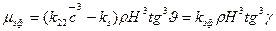(8.53)

где

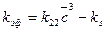(8.54)

Силу сопротивления, действующую на погружающийся конус со стороны жидкости, можно представить в виде

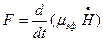(8.55)

При выводе формул для 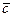, а следовательно, и для μ_эф использовалось свойство автомодельности течения около конуса, которое строго справедливо лишь при 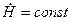; либо при 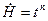. Однако при малых ускорениях 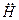, что характерно для стадии проникания, скорость приближенно можно считать зависящей от времени по произвольному закону. Поэтому приближенно справедливо выражение

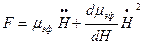(8.56)

В случае погружения с постоянной скоростью (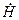= 0) сила сопротивления пропорциональна квадрату глубины погружения:

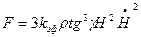(8.57)

Если конус имеет конечную высоту и радиус его донного среза равен R, то сила сопротивления примет максимальное значение, ког­да свободная поверхность жидкости достигнет плоскости донного среза конуса. На рис. 8.7 приведены результаты численного расчета коэффициента сопротивления 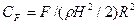двух конусов (γ = 45° и γ= 30°) в зависимости от Н/R методом крупных частиц (сплошные линии). Как видим, увеличение угла заострения приводит к резкому возрастанию нагрузок и уменьшению времени на­растания максимальной нагрузки. На этом же рисунке кружочка­ми обозначены результаты расчета по приведенной приближенной методике с использованием эквивалентного эллипсоида. На рис. 8.8 приведены расчетные значения k_эф и экспериментальные дан­ные различных авторов.

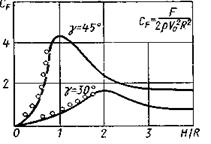
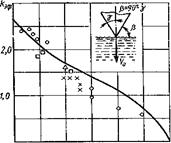
Рис. 8.7 Рис. 8.8

Приближенная методика охватывает весь диапазон углов γ, хотя при малых значениях γ наблюдается превы­шение расчетных значений над экспериментальными.