Несимметричное погружение конусов

НЕСИММЕТРИЧНОЕ ПОГРУЖЕНИЕ В ВОДУ ТЕЛ ВРАЩЕНИЯ

Несимметрия течения при погружении в воду тел вращения мо­жет быть вызвана либо наличием угла атаки при вертикальном входе, либо отклонением траектории входа от вертикали. Оба фактора могут присутствовать и одновременно.

Нарушение осевой симметрии течения приводит к ряду своеоб­разных явлений. Прежде всего помимо осевых сил сопротивления возникают значительные поперечные нагрузки. Нарастание осе­вых нагрузок по времени при наклонном входе происходит медлен­но, максимальные нагрузки снижаются. Это обусловлено тем фак­том, что свободная поверхность может деформироваться и как быамортизировать ударные нагрузки. В условиях несимметричного по­гружения удлиненное тело получает угловые перемещения относи­тельно центра масс. Вследствие этого траектория погружения от­клоняется от прямолинейной в сторону меньших глубин. При не­симметричном входе существенно изменяются условия кавернообразования и замыкание каверны. Как правило, поверхностное смыкание затрудняется, а движение тела в развитой каверне со­провождается глиссированием кормовой части по поверхности ка­верны. При определенных условиях может возникнуть рикошет.

Рассмотрим характерис­тики поперечной силы, обусловленной углом атаки. При малых уг­лах γ (острые конусы) и малых углах атаки коэффициент попереч­ной силы будет приблизительно определяться формулами линей­ной теории, а в пределе — теорией тонкого тела:

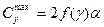, (8.63)

где

.

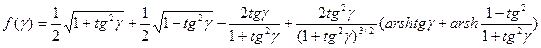Функция f(γ) отражает влияние конечного значения угла γ и в пределе при γ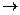0 стремится к единице.

При больших углах γ (затупленные конусы) поперечная сила может быть оценена по аналогии с горизонтальным ударом экви­валентного эллипсоида вращения со скоростью 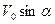. Может быть использован также метод конических сегментов, согласно ко­торому погружающийся конус разбивается радиальными плоско­стями на ряд конических сегментов и распределение давления на каждом из таких сегментов такое же, как на вертикально погру­жающемся конусе с эквивалентным углом конусности. Этот угол для каждого сегмента будет разный. В предельном случае γ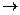-л;/2 и α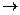0. Такой подход дает простую оценочную формулу

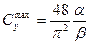, где 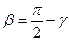. (8.64)

При конечных значениях угла атаки а характеристика С_у^mах(α) является нелинейной. Максимальные нагрузки достигаются при 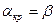, когда первоначальный удар происходит вдоль образующей конуса (рис. 8. 12).

Максимальная осевая сила (сила сопротивления) имеет наи­большее значение при нулевом угле атаки. С ростом угла атаки она падает, а затем достигает вто­рого пика при 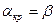(рис. 8.13).

Отличие траектории от верти­кальной в случае острых конусов

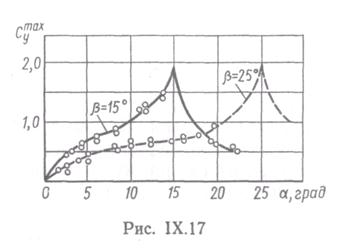
не приводит к появлению заметных боковых сил. Для тупых кону­сов влияние угла входа θ аналогично влиянию угла атаки на боко­вые силы. Чем больше угол входа θ, тем выше максимальное зна­чение силы сопротивления. Качественная картина протекания ха­рактеристик показана на рис. 8.14.