Проникание сферы

Уравнение меридионального сечения сферы имеет вид

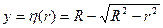(8.58)

Для построения приближенных методик расчета гидродинами­ческих нагрузок использовались различные эквивалентные тела: диск, сферические линзы, трехосный эллипсоид. В последнем случае за вертикальную полуось эллипсоида принималась глубина погруже­ния, за одну горизонтальную полуось принимался радиус сфериче­ского сегмента в плоскости невозмущенной жидкости, а другая полуось в перпендикулярном направлении находилась из условия равенства объема эллипсоида и погруженной части сферы. Встреч­ное движение жидкости пои этом не учитывалось.

На рис. 8.9 и 8.10 представлены за­висимости безразмерной силы сопротивления 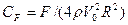и безразмерной скорости 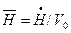, где V₀ — скорость приводнения от

Рис.8.10

Рис.8.9

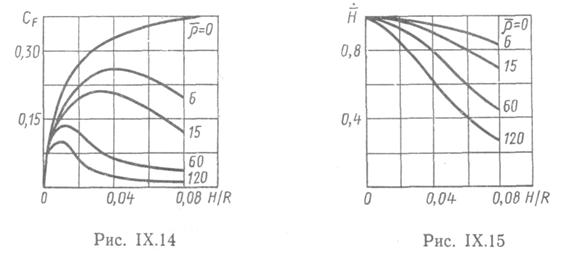относительного погружения 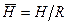при различных значениях относительной плотности 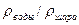и малых значениях 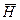. Случай 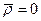соответствует бесконечно большой собственной массе шара, вследствие чего погружение происходит с постоянной скоростью. Если плотность шара невелика, то наблюдается заметное торможение шара. Результаты расчета 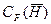в общем удовлетворитель­но совпадают с опытными данными в диапазоне 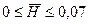, хотя на нарастающей ветви кривой расчетные результаты заметно пре­вышают экспериментальные.

При погружении с постоянной скоростью возможно приближен­ное получение явной зависимости коэффициента сопротивления от относительного погружения вида

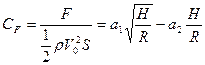(8.59)

Эксперименты позволили уточнить значения констант а₁ и а₂, и в диапазоне 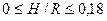формулу (8.59) можно представить в виде

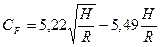(8.60)

При погружениях 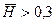на сфере формируется каверна и последующая нагрузка резко падает.