Пусть диск погружается в воду под углом θ и скорость приводнения V0 отклонена на угол атаки а от нормали к его поверхности (рис. 8.16). После касания невозмущенной поверхности воды нижней кромкой диска возникают брызговые
|
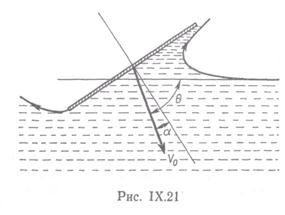
струи, основания которых распространяются вдоль кромок диска. Сопротивление формируется за счет нестационарности процесса и за счет распределения давления на диске, которое соответствует квадратичному члену в интеграле Коши — Лагранжа:
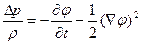 (8.65)
(8.65)
Стадия проникания завершается, когда основание брызговых струй достигает верхней кромки диска. Вместо времени удобно ввести величину погружения, отсчитываемую вдоль диаметра диска. Очевидно, геометрическое соотношение
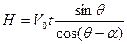 (8.66)
(8.66)
Опираясь на представление, что нестационарная часть сопротивления отождествляется с понятием присоединенной массы, а другая часть напоминает «кавитационное» сопротивление, можно сконструировать полуэмпирическую зависимость силы сопротивления вида
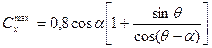 , (8.67)
, (8.67)
пригодную в диапазоне | α|<20°, 40°<θ<86°. Ясно, что формула исключает случай θ-α =90°, поскольку в рамках несжимаемой жидкости это должно приводить к бесконечным значениям силы. В этом случае нужно вводить поправку на сжимаемость воды:
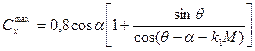 (8.68)
(8.68)
где на основании экспериментальных данных найдено k1= 0,35. Время нарастания максимальной нагрузки определяется зависимостью
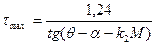 (8.69)
(8.69)
где 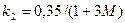
 2014-02-02
2014-02-02 443
443








