Нагрузки на переходной стадии

После того как произойдет от­рыв основания брызговых струй от поверхности погружающегося тела, сила сопротивления начинает резко уменьшаться и стремить­ся к стационарному значению кавитационного сопротивления. Рас­чет нагрузок на переходной стадии успешно осуществляется числен­ными методами. Пример такого расчета приведен на рис. 8.6.

Приближенная оценка может быть выполнена с помощью пе­реходной функции Г. В. Логвиновича, которая на левом конце пе­реходной стадии обеспечивает значение максимальной силы, а на правом - кавитационное сопротивление при числе кавитации, рав­ном нулю. Вывод выражения для переходной функции конуса ос­нован на теории ударного погружения диска, радиус которого с>R находят из условия: на кромке диска с=R перепад давления об­ращается в ноль. В подвижной системе координат на поверхности фиктивного диска с>R:

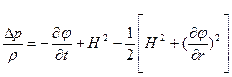(8.74)

Положив Δр=0 и подставив соответствующие значения потен­циала, найдем дифференциальное уравнение для нахождения с(t):

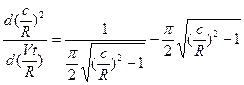(8.75)

с начальным условием: при t=0 с/R=1. Интегрирование дает

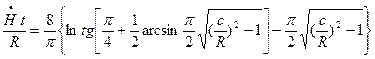
Последующее интегрирование (1Х.74) дает значение силы в виде двух слагаемых:

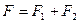. (8.76)

где

;

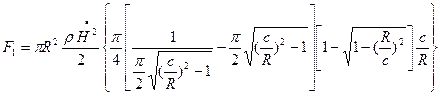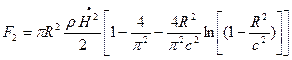. (8.77)

Составляющая F₁ с ростом глубины погружения, монотонно убы­вая, стремится к нулю. Вторая составляющая при безграничном росте глубины стремится к конечному значению 0,7. Заметим, что при неограниченном росте глубины погружения величина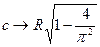

Для того чтобы удовлетворить граничному условию на правом конце, сконструируем переходную функцию в виде

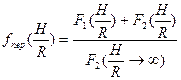(8.78)

Тогда

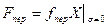. (8.79)

Граничное условие на левом конце удовлетворим, выбрав соответствующее начало отсчета времени в переходной функции из условия

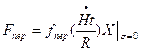(8.80)

Аналогичный подход применяется и для построения переход­ной функции при погружении клина. Разница заключается лишь в использовании теории ударного по­гружения пластины.

Эффективность изложенных при­ближенных методов демонстрирует­ся на примере поперечного погру­жения кругового цилиндра (рис. 8.17).

Коэффициент сопротивле­ния 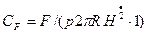рассчитан, по теории эквивалентного эллиптического цилиндра (пунктир­ная линия) и по переходной функ­ции (штрихпунктирная линия).

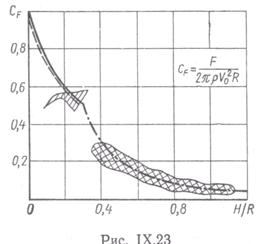
Заштрихованные области соответству­ют экспериментальным данным. Наибольшая неопределенность существует в области предельно малых погружений. Трудности регистрации момента касания во­ды и соответствующего измерения сил не позволяют получать до­стоверные опытные данные в этой зоне.