Глиссирование крыла

Рис.9.1

Диаграмма избыточного давления также показана на рис. 9.1. Как видим, избыточное давление существует на нижней стороне пластины от точки разворота свободной поверхности до задней кромки. Этот участок носит название смоченной длины пластины. Участок же пластины, омываемый брызговой струей, несущей спо­собностью не обладает, так как давление в брызговой струе равно давлению окружающей атмосферы. Помимо сил давления на пла­стину действуют также силы трения, обусловленные вязкостью во­ды. При этом интересно отметить, что поток в носовой части пла­стины, развернувшийся навстречу набегающему потоку, создает силу трения, направленную вперед. Правда, это тянущее усилие становится заметным начиная лишь с углов атаки а 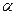>4...6°. На остальном протяжении пластины (вниз по потоку от критической точки) вязкие силы создают силу сопротивления трения.

Продольная сила в связанной системе координат равна

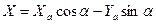. (9.1)

а сила сопротивления в скоростной системе координат

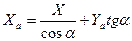. (9.2)

Продольная сила Х полностью определяется вязкими силами и может быть определена методами пограничного слоя. Второе сла­гаемое в формуле (9.2) представляет собой сопротивление давле­ния, обусловленное возникновением брызговой струи (брызговое сопротивление) и волнообразованием (волновое сопротивление). В условиях стационарного движения реализуется равенство

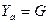, (9.3)

так что

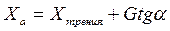, (9.4)

где

, .

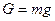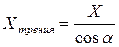Гидродинамический момент при глиссировании рассчитывают относительно задней кромки:

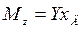, (9.5)

где 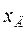— координата центра давления.

Поскольку смоченная длина пластины 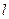является величиной пе­ременной, в качестве характерного линейного размера обычно принимают ширину В (размах) пластины. Если удлинение пластины 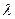= B /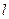, то безразмерная координата центра давления равна

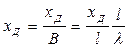. (9.6)

Задача являет­ся плоской и поэтому допускает применение теории функций ком­плексного переменного. К настоящему времени известны решения при немалых углах атаки (нелинейная задача), учете весомости воды, различном искривлении пластины, наличии механизации на задней кромке и т. д. Не останавливаясь на сложных теоретических решениях, укажем один полезный практический прием, пригодный при малых углах атак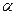и и .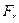

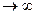Рассмотрим линеаризованную задачу о глиссировании пластины. Потенциал возмущенных скоростей должен удовлетворять уравне­нию Лапласа:

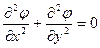. (9.7)

На свободной поверхности у=f(х) должны выполняться два граничных условия: динамическое и кинематическое. Динамическое условие требует, чтобы на свободной поверхности давление равня­лось атмосферному. Но тогда из уравнения Бернулли следует

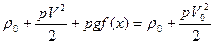. (9.8)

Выразим квадрат скорости:

.

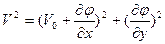Подставим это выражение в уравнение Бернулли и отбросив производные в степени выше первой, найдем линеаризованную фор­му динамического условия на свободной поверхности:

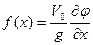
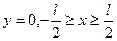. (9.9)

Кинематическое условие dS/dt=0, где S=у—f(х t), в развер­нутом виде примет вид

.

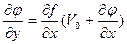После линеаризации получим

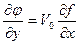. (9.10)

Производную df/dх получим из линеаризованного кинематиче­ского условия. Тогда

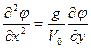
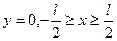. (9.11)

Установим теперь граничные условия на пластине. В силу тангенциальности потока

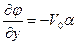
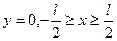. (9.12)

На задней кромке должен быть обеспечен плавный сход струй. Ос­тается теперь записать условие на бесконечности:

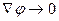при 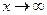(9.13)

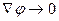при 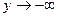(9.14)

Сформулированная задача остается еще достаточно сложной. Однако упростим ее еще более, положив .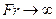

Запишем динамическое условие в безразмерном виде:

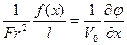
При 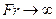следует, что на свободной поверхности y=0, -l/2 ≥ x≥ l/2 справедливо d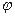/dх=0 или 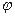=const. Без потери общности можно положить

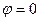(9.15)

Как и в задаче об ударе, это условие позволяет продолжить не­симметричным образом потенциал в верхнюю полуплоскость 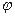(x, у)=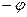(x,-у) и свести задачу о глиссировании пластины по поверхности воды к задаче обтекания пластины под углом атаки безграничным потоком жидкости.

Линеаризованная форма уравнения Бернулли дает соотношение для избыточного давления на верхней и нижней стороне пластины:

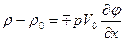. (9.16)

На нижней стороне наблюдается повышение давления, а на верхней — разрежение. При движении в безграничном потоке ре­зультирующая сила создается в результате суммирования этих дав­лений. При глиссировании давление на верхней поверхности посто­янно (разрежения нет) и нормальная сила создается только за счет повышения давления на нижней стороне пластины. Следовательно, нормальная сила глиссирующей пластины будет вдвое меньше, чем у пластины в безграничном потоке:

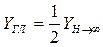, (9.17)

где 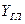— подъемная сила глиссирующей пластины; Y 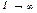— подъ­емная сила пластины в безграничной жидкости (на бесконечной глубине).

При обтекании острой кромки должны разви­ваться бесконечные скорости, а соответственно отрицательные дав­ления. Произведение бесконечного разрежения на бесконечно ма­лую носовую площадку дает конечную величину, называемую под­сасывающей силой. В реальных условиях бесконечных разрежений быть не может. Поток срывается и на верхней поверхности у перед­ней кромки образуется носовой пузырь. В такой ситуации картина течения близка к условиям глиссирования.

Аналогия Вагнера позволяет использовать хорошо разработан­ную теорию профиля в потоке безграничной жидкости. В частности, для профиля известно решение

.

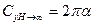Следовательно,

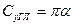. (9.18)

Аналогия Вагнера справедлива не только для профиля, но и для крыла конечного размаха. При этом опять-таки углы атаки должны быть малы, а передние кромки крыльев острыми. Глис­сирующее крыло является частным случаем подводного крыла, ха­рактеристики которого зависят от глубины по закону

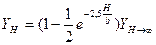, (9.19)

где b — хорда крыла.

Для расчета величины подъемной силы глиссирующего крыла необходимо знать смоченную длину l, которая пока не известна.

Для ее определения можно воспользоваться примерно тем же под­ходом, что и при определении величины подпора от встречного дви­жения воды в задаче о входе в воду. Подъем свободной поверхно­сти можно выразить в виде

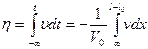, (9.20)

где 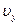- вертикальная скорость жидких частиц на свободной по­верхности; 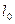- расстояние от задней кромки пластины до уровня невозмущенной свободной поверхности, измеряемое вдоль пла­стины.

С другой стороны, из геометрических соображений непосредст­венно следует

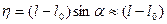. (9.21)

Таким образом, после приравнивания (9.20) и (9.21) получаем интегральное уравнение для нахождения неизвестной смоченной длины:

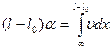. (9.22)

Вертикальную скорость 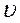нужно выразить с помощью опреде­ленной схемы обтекания крыла. Как уже отмечалось, для крыла конечного размаха простейшей является схема одиночного П -образного вихря. Более сложной является схема несущей линии. А в общем случае можно рассматривать схему несушей поверхности, применяя затем метод дискретной вихревой решетки. На практике использовались все указанные подходы.

В случае одиночного подковообразного вихря скос потока от присоединенного вихря равен

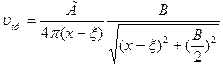, (9.23, а)

а от свободных вихрей

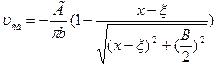. (9.23, б)

Выполнив интегрирование в (9.22), придем к соотношению

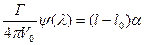, (9.24)

где

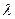; =B/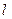

Величину циркуляции Г можно выразить через принятую зави­симость для коэффициента подъемной силы крыла. Наиболее про­стой формулой является

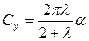. (9.25)

Следовательно, справедливо соотношение

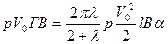. (9.26)

откуда следует

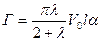. (9.27)

Подставляя это значение циркуляции в (9.24), получаем тран­сцендентное уравнение для определения смоченной длины пласти­ны:

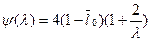, (9.28)

где =/

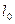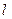
Анализ уравнения показывает, что решения получаются при про­извольных знаках . При =0 (задняя кромка касается воды) 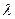=7,9, при <0 задняя кромка приподнята над невозмущенной поверхностью воды (при = -0,0275 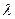=22,5), при >0 задняя кромка опущена ниже невозмущенной поверхности воды. Вообще же, для нахождения 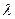, при определенных значениях параметра нужно решать уравнение (9.28).