При теплоотдаче (или конвективном теплообмене) тепло передается за счет перемещения частиц теплоносителя. Движение частиц теплоносителя может происходить под действием внешнего перепада давлений (вынужденная конвекция) или за счет разности плотностей частиц с разной температурой (свободная или естественная конвекция). Интенсивность переноса тепла определяется распределением температур, свойствами теплоносителя, размерами, формой и ориентацией поверхности теплоотдачи. Процесс конвективного теплообмена описывается основным уравнением теплоотдачи:
Q=aFtÑt, (2.17)
где a – коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2×К).
Коэффициент теплоотдачи численно равен количеству тепла, передаваемому между теплоносителем и стенкой площадью в один квадратный метр за одну секунду при температурном напоре в один градус. Численные значения коэффициента теплоотдачи колеблются в широких пределах от нескольких десятков кВт/(м2×К) до нескольких Вт/(м2×К). Большие значения относятся к воде и жидким металлам при вынужденной конвекции, малые – к газам при свободной конвекции.
Процесс нестационарной теплоотдачи описывается дифференциальным уравнением конвективного теплообмена Фурье-Кирхгофа. Это дифференциальное уравнение получается аналогично дифференциальному уравнению нестационарной теплопроводности. В статью прихода теплового баланса элементарного параллелепипеда добавляется тепло, вносимое потоками теплоносителя, проходящими через грани параллелепипеда:
dQК=dx dy dz dt rс[¶(wхt)/¶z+¶(wyt)/¶y+¶(wzt)/¶z]=
=dxdydzdtrс[t(¶wx/¶z+¶wy/¶y+¶wz/¶z)+wx¶t/¶z+wy¶t/¶y+wz¶t/¶z].
Сумма производных ¶wx/¶z+¶wy/¶y+¶wz/¶z, согласно уравнению неразрывности потока (4.31), равна нулю.
Преобразования уравнения теплового баланса приводят к уравнению
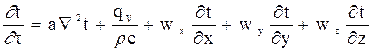 , (2.18)
, (2.18)
где wx, wy, wz – скорости по осям координат, м/с.
Интегрирование дифференциального уравнения даже для простейших случаев связано со значительными трудностями, а для большинства практических задач невозможно. По этой причине для расчетов коэффициента теплоотдачи используются полуэмпирические критериальные уравнения, полученные методом подобных преобразований.
После зачеркивания знаков дифференцирования в уравнении (2.9), записанном для случая отсутствия внутренних источников тепла (qv=0), получим t/t+wt/L»at/L2. Приведем полученное выражение к безразмерному виду, разделив обе части выражения на at/L2 :
tL2/a+wL/a»1. (2.19)
Первый член выражения (2.18) является критерием Фурье, который является безразмерным временем и используется в расчетах нестационарных тепловых процессов:
Fo=tL2/a. (2.20)
Второй член выражения (2.19) является критерием Пекле wL/a=Ре, который характеризует тепловые процессы. Обычно он используется в сочетании с критерием Рейнольдса.
Тепловые процессы описываются системой дифференциальных уравнений Фурье-Кирхгофа и Навье-Стокса, а также граничными условиями. Подобные преобразования уравнения Навье-Стокса (см. п.4.3) приводят к критериям гомохронности (Но), Эйлера (Eu), Рейнольдса (Re) и Фруда (Fr). Первые два критерия не оказывают влияния на тепловые процессы и используются при решении чисто гидравлических задач.
Граничным условием тепловых процессов является равенство тепловых потоков теплопроводности пограничного слоя теплоносителя и теплоотдачи q=aÑt=ldt/dx. После зачеркивания знаков дифференцирования и приведения к безразмерному виду, получим определяемый критерий тепловых задач – критерий Нуссельта
Nu=aL/l. (2.21)
Критерий Нуссельта характеризует теплообмен в пограничном слое.
Решением системы дифференциальных уравнений, описывающих тепловой процесс, является критериальное уравнение
Nu=f(Re,Fr,Pe,Fo). (2.22)
Использование критерия Пекле во многих случаях неудобно, т.к. он включает в себя скорость потока. Вместо него используется отношение критериев Пекле и Рейнольдса, получившего название критерия Прандтля
Pr=Pe/Re=n/a, (2.23)
который отражает влияние теплофизических свойств теплоносителя на теплоотдачу.
При свободной конвекции режим движения теплоносителя определять по значениям числа Рейнольдса невозможно, т.к. скорость движения определять сложно. По этой причине для отражения влияния на тепловой процесс режима свободного движения теплоносителя используется критерий Аpхимеда Ar=gL3Ñr/(rv2), в котором отношение разности плотностей среды и частицы к плотности среды Ñr/r заменено произведением температурного напора на коэффициент термического расширения теплоносителя bÑt. Такой модифицированный критерий Аpхимеда называется критерием Грасгофа и характеризует режим движения теплоносителя при свободной конвекции:
Cr=gL3bÑt/v2. (2.24)
Общее для всех тепловых процессов критериальное уравнение, с введением параметрических критериев Г1 и Г2, будет иметь вид
Nu=f(Re,Сr,Pr,Fo,Г1,Г2). (2.25)
Для отдельных случаев теплообмена уравнение (2.25) упрощается. При стационарном ходе процесса опускается критерий Фурье. При отсутствии вынужденного движения теплоносителя из уравнения исключается критерий Рейнольдса. Так как температура пограничного слоя отличается от температуры ядра потока, следовательно, и физические свойства также будут отличаться от соответствующих параметров основного потока. Так, при нагревании вязкость пограничного слоя будет ниже, чем у основного потока. В результате чего скорость пограничного слоя окажется больше той, которая бы наблюдалась у изотермического потока. По этой причине коэффициент теплоотдачи при нагревании жидкостей будет больше, чем при их охлаждении. Кроме изменения вязкости в пограничном слое изменяются и другие физические константы. Учет влияния этого фактора проводится введением в критериальное уравнение отношения Pr/Prст, в котором критерий Pr выбирается при средней температуре теплоносителя, а Prст – для теплоносителя при средней температуре стенки. Для газов изменения вязкости компенсируются изменениями теплоемкости, теплопроводности и плотности, и поэтому критерий Прандтля мало зависит от температуры, а отношение Pr/Prст»1.
Таким образом, для свободной конвекции критериальное уравнение имеет вид
Nu=C(Pr Cr)n(Pr/Prст)0,25, (2.26)
где Prст=n/a – критерий Прандтля для теплоносителя в пограничном слое (определяется при средней температуре стенки); С, n, k – эмпирические константы, зависящие от вида поверхности и режима теплоотдачи.
Режим свободной конвекции определяется по значениям произведения критериев Прандтля и Грасгофа.
На рисунке 2.4 приведена схема естественных токов теплоносителя у вертикальной горячей стенки. Пограничный ламинарный слой теплоносителя начинает формироваться у нижней кромки стенки. По мере подъема его толщина, за счет вовлечения в движение новых порций теплоносителя, увеличивается (зона I). Одновременно растет и скорость движения.
 При достаточно больших значениях скорости ламинарный поток распадается на два подслоя: ламинарный 1 и турбулентный 2. На некотором расстоянии идет стабилизация режима движения и поток движется в переходном режиме (зона II). В верхней части стенки режим движения потока турбулентный (зона III). При этом у стенки остается гидравлический пограничный слой, движущийся ламинарно. Распределение температур по нормали к стенке в ламинарно движущемся теплоносителе линейное, в турбулентном потоке криволинейное (см.рис.2.4,в).
При достаточно больших значениях скорости ламинарный поток распадается на два подслоя: ламинарный 1 и турбулентный 2. На некотором расстоянии идет стабилизация режима движения и поток движется в переходном режиме (зона II). В верхней части стенки режим движения потока турбулентный (зона III). При этом у стенки остается гидравлический пограничный слой, движущийся ламинарно. Распределение температур по нормали к стенке в ламинарно движущемся теплоносителе линейное, в турбулентном потоке криволинейное (см.рис.2.4,в).
В соответствии с изменением толщины и режима движения пограничного слоя изменяются локальные значения коэффициента теплоотдачи. В ламинарной зоне коэффициент теплоотдачи уменьшается, т.к. возрастает толщина пограничного слоя и, следовательно, увеличивается его термическое сопротивление. В переходной зоне, в связи с уменьшением толщины ламинарно движущегося потока, коэффициент теплоотдачи растет. В турбулентной зоне гидравлический пограничный слой стабилизирован и коэффициент теплоотдачи практически постоянен (см.рис.2.4,б). Средние значения коэффициента теплоотдачи для стенки определяются по критериальному уравнению (2.26).
В качестве определяющего размера в критериальных уравнениях используется размер поверхности по вертикали: для горизонтальных плит – размер меньшей стороны, горизонтальных стержней и труб – диаметр. Определяющей температурой является температура теплоносителя вдали от поверхности теплообмена. Значения критерия Prст берутся для теплоносителя при температуре стенки. Для газов критерий Прандтля мало зависит от температуры, и отношение Pr/Prст можно считать равным единице.
При теплоотдаче внутри замкнутых объемов (узких щелях, плоских и кольцевых зазорах) при (Pr Cr)>1000 образуется серия циркуляционных токов. И в этом случае физические свойства выбираются при средних температурах стенок, в качестве определяющего размера используется толщина зазора и принимается Pr=Prст.
Таблица 2.1
Значения эмпирических констант в формуле (2.26)
| Случаи теплоотдачи | (Cr×Pr) | А | n |
| Вертикальные поверхности | 103...109 | 0,76 | 0,25 |
| То же | >109 | 0,15 | 0,33 |
| Горизонтальные цилиндры. Сфера | 103...108 | 0,50 | 0,25 |
| Горизонтальные плиты (горячие, обращенные вверх, и холодные, обращенные вниз) | 105...2×107 | 0,54 | 0,25 |
| То же | 2×102...3×1010 | 0,14 | 0,33 |
| Горизонтальные плиты (горячие, обращенные вниз, и холодные, обращенные вверх) | 105...2×107 | 0,27 | 0,25 |
| То же | 2×102...3×1010 | 0,07 | 0,33 |
| Узкие щели | >1000 | 0,18 | 0,25 |
При (Pr Cr)<1000 в узких щелях свободное движение теплоносителя практически отсутствует и тепло передается теплопроводностью. Если горячая поверхность в горизонтальных щелях располагается сверху, то конвекция также отсутствует.
При вынужденной конвекции перенос тепла происходит за счет движения теплоносителя, вызванного действием внешнего перепада давлений. Интенсивность переноса тепла определяется распределением температур, режимом движения и свойствами теплоносителя, размерами, формой и ориентацией поверхности теплоотдачи. Численные значения коэффициента теплоотдачи при вынужденной конвекции колеблются в широких пределах от нескольких десятков кВт/(м2×К) до нескольких десятков Вт/(м2×К). Большие значения относятся к воде и жидким металлам, малые – к газам.
Рассмотрим некоторые частные случаи вынужденной конвекции.
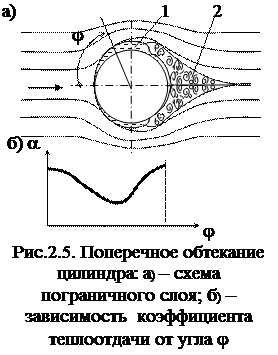
При поперечном обтекании цилиндрических поверхностей (рис. 2.5,а) набегающий поток огибает поверхность цилиндра и создает на его поверхности гидравлический пограничный слой 1. Толщина этого слоя минимальна в лобовой части. По мере ухода от лобовой части она растет и достигает максимальных значений при j=95¼105°. В этом месте наблюдается срыв пограничного слоя, и в кормовой части возникает турбулентная зона 2, образующая кормовой след. Толщина гидравлического ламинарного пограничного слоя в кормовой части уменьшается. В соответствии с изменениями толщины гидравлического пограничного слоя изменяются и локальные значения коэффициента теплоотдачи (рис. 2.5,б). При ламинарном набегающем потоке коэффициент теплоотдачи ниже, чем в лобовой части, а при движении теплоносителя в турбулентном режиме соотношение между локальными значениями в лобовой и кормовой части меняется на противоположное. Средние значения коэффициента теплоотдачи определяются из критериального уравнения.
 Nu=ARenPrm(Pr/Prст)0,25ejen. (2.27)
Nu=ARenPrm(Pr/Prст)0,25ejen. (2.27)
При обтекании одиночных труб и их пучков в критериальные уравнения вводится поправочный коэффициент на угол атаки (угол между вектором скорости теплоносителя и осью труб) ej. Для углов атаки j=90°, 70°, 50° и 30° поправочный коэффициент ej равен 1,0, 0,98, 0,88 и 0,67, соответственно. При омывании труб и их пучков с углами атаки j<10° расчет ведут по уравнениям для каналов.
При переходе от предшествующего ряда труб пучка к последующему коэффициент теплоотдачи увеличивается. Начиная с третьего ряда это увеличение незначительно, поэтому по критериальным уравнениям находится коэффициент теплоотдачи для третьего и последующих рядов пучка. Поправочный коэффициент на число рядов определяется по формуле
en=[0,6n1+an2+(n-n1-n2)]/n, (2.28)
где n1, n2 и n – число труб в первом ряду, во втором и пучке в целом; а – константа, учитывающая тип пучка (для коридорных пучков а=0,9 и для шахматных а=0,7). Интенсивность теплоотдачи в шахматных пучках выше, чем в коридорных. В шахматных пучках трубы предшествующего ряда направляют поток на трубы последующего ряда, а в коридорном пучке трубы предшествующих рядов заслоняют последующие трубы и степень турбулизации потока теплоносителя снижается. Это обстоятельство учитывается константами критериальных уравнений.
Расчет коэффициента теплоотдачи при вынужденной конвекции проводится по критериальным уравнениям вида:
– для газов и жидкостей в трубах и каналах
Nu=ARenPrmСrk(Pr/Prст)0,25e1e2; (2.29)
– для жидких металлов в трубах и каналах
Nu=A+nPem; (2.30)
– для аппаратов с мешалками
Nu=AReмnPrm(m/mст)k; (2.31)
– для пленочного течения жидкостей
Nuпл=ARenплPrm(dпр/Н)k; (2.32)
– между теплоносителем и слоем зернистого материала
Nuо=A(Reо/e)nPrm; (2.33)
– между газом и жидкой пленкой, стекающей по насадке
Nu=AReоnRe mжPrkж, (2.34)
где e1, e2 – поправочные коэффициенты на учет факторов, не вошедших в дифференциальные уравнения (участок тепловой и гидравлической стабилизации, кривизна потока, расположение труб в трубной решетке и др.); А, k, n и m – эмпирические константы, зависящие от вида поверхности теплоотдачи и режима движения теплоносителя (табл.2.2); Nuпл=adпр/l и Reпл=4Г/m – модифицированные критерии Нуссельта и Рейнольдса для пленки; dпр=(n2/g)0,33 – приведенная толщина пленки; Н – высота стенки (трубы); Nuо=ado/l и Reо=wodo/n – модифицированные критерии Нуссельта и Рейнольдса для слоя зернистого материала; dо и e – диаметр частиц и порозность слоя зернистого материала; Reж=4G/(am) – модифицированный критерий Рейнольдса для жидкости, орошающей насадку; а – удельная поверхность насадки; G – массовый расход жидкости.
Остановимся на механизме влияния факторов, не учтенных в дифференциальных уравнениях и учитываемых в критериальных уравнениях поправочными коэффициентами.
При движении теплоносителя в трубах и каналах вводится поправка на участок тепловой и гидравлической стабилизации eL/d, на котором идет формирование теплового и гидравлического пограничных слоев. Этот участок находится между входным сечением канала и сечением, в котором отсутствуют частицы теплоносителя с температурой, равной его температуре на входе в канал. На этом участке толщина пограничных слоев растет, следовательно, термическое сопротивление теплоотдаче увеличивается и коэффициент теплоотдачи уменьшается. За пределами участка тепловой стабилизации коэффициент теплоотдачи практически не изменяется. Учет влияния этой поправки проводят только для коротких труб и каналов, у которых отношение длины к эквивалентному диаметру меньше 50. При ламинарном режиме движения eL/d=(L/d)0,4. Для турбулентного режима движения величина поправочного коэффициента достигает 1,65, зависит от критерия Рейнольдса и отношения L/d и её значения приводятся в литературе [17].
В изогнутых трубах и каналах за счет дополнительной турбулизации потока под действием центробежных сил наблюдается увеличение коэффициента теплоотдачи (по сравнению с течением по прямолинейным траекториям). Это увеличение коэффициента теплоотдачи учитывается поправочным коэффициентом на кривизну трубы, определяемым по формуле
ed/R=1+1,77dэ/R, (2.35)
где dэ и R – эквивалентный диаметр канала и его радиус кривизны.
Для вертикальных каналов иногда учитывается влияние направлений свободного и вынужденного движений теплоносителя. При совпадении их направлений рекомендуется увеличивать, а в случае противоположности направлений уменьшать коэффициент теплоотдачи на 5¼10%.
Таблица 2.2
Значения эмпирических коэффициентов в формулах (2.27) и (2.34)
| Форма поверхности и потока | Границы применения | Формула | А | n | m | k |
| В трубах и каналах | Re<2320 | 2.29 | 0,15 | 0,33 | 0,43 | 0,1 |
| Re=2320...104 | 0,008 | 0,9 | 0,43 | - | ||
| Re>10000 | 0,021 | 0,8 | 0,43 | - | ||
| Обтекание плиты | Re<105 | 0,66 | 0,5 | 0,33 | - | |
| Re>105 | 0,037 | 0,8 | 0,43 | - | ||
| Обтекание трубы | Re=5...103 | 0,5 | 0,5 | 0,38 | - | |
| Re=103...2×105 | 0,25 | 0,6 | 0,38 | - | ||
| Re=(2...20)×105 | 0,023 | 0,8 | 0,37 | - | ||
| Обтекание пучка труб | Re<103 | 2.27 | 0,56 | 0,5 | 0,36 | - |
| Коридорный пучок | Re>103 | 0,22 | 0,65 | 0,36 | ||
| Шахматный пучок | Re>103 | 0,4 | 0,6 | 0,36 | ||
| Жидкие металлы | Re=20...104 | 2.30 | 4,56 | 0,025 | 0,08 | |
| Аппараты с листовыми мешалками к стенке | 2.31 | 0,36 | 0,67 | 0,43 | 0,14 | |
| То же к змеевику | 0,87 | 0,62 | 0,43 | 0,14 | ||
| То же с якорными мешалками (dм/D=0,94) | Re<40 | 0,003 | 0,9 | 0,68 | 0,7 | |
| Вертикальная стенка | Re<2320 | 2.32 | 0,67 | 0,11 | 0,33 | 0,33 |
| Re>2320 | 0,01 | 0,33 | 0,33 | |||
| Горизонтальный пучок труб с поперечным шагом S1/dн=1,7¼2 | 0,005 | 0,33 | 0,33 | |||
| Слой зернистого материала | Reo/e<200 | 2.33 | 0,0035 | 1,5 | 0,33 | - |
| Reo/e>200 | 0,4 | 0,67 | 0,33 | - | ||
| Псевдоожиженный слой | Reo/e<200 | 0,016 | 1,3 | 0,33 | - | |
| Reo/e>200 | 0,4 | 0,4 | 0,33 | - | ||
| Для воздушных скрубберов | 2.34 | 0,01 | 0,7 | 0,7 | 0,33 |
Для определения коэффициента теплоотдачи при вынужденном движении теплоносителей в каналах в переходном режиме (Re=2100¼10000) надежных формул нет. При проектных расчетах рекомендуется этот режим избегать, изменяя скорости теплоносителей (или сечение аппаратов). Если же этого не удается, то можно воспользоваться критериальным уравнением (2.36), для которого в таблице 2.3 приведены значения постоянного сомножителя.
Nu=KoPr0,43(Pr/Prст)0,25, (2.36)
где Ко – функция от критерия Рейнольдса.
Таблица 2.3
Постоянный сомножитель Ко
| Re | |||||||||||
| Ko | 1,9 | 2,2 | 3,3 | 3,9 | 4,4 | 6,0 | 10,3 | 15,5 | 19,5 | 27,0 | 33,3 |
 2014-02-02
2014-02-02 4412
4412
