Кодирование информации сверточными кодами

Задание систематических сверточных кодов

Систематические СК задаются:

I. с помощью порождающей матрицы – G _¥(х);

II. с помощью проверочной матрицы – H _¥(х);

III. с помощью разностных треугольников;

IV. с использованием совершенных разностных множеств.

I. Задание систематических СК с помощью порождающей матрицы G_¥(х)

Порождающая матрица систематического СК имеет более сложное построение, чем у группового кода. Это определяется из-за полубесконечной структуры порождающей матрицы СК, имеющей вид:

где "0" - области матрицы, состоящие полностью из нулевых двоичных символов,

т - количество порождающих матриц вида

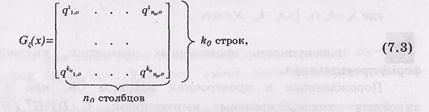
где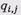 – коэффициенты равны либо 1, либо 0.

Систематический ССК задаются следующей порождающей матрицей G_¥(х):

II. Задание систематических СК с помощью проверочной матрицы H_¥(х)

Проверочная матрица Н_¥(х) СК, как и порождающая матрица, является полубес­ко­нечной:

- совокупность проверочных подматриц, имеющих форму треугольника.

Порождающая и проверочная матрицы СК, как и у линейных кодов, связаны выражением: G_¥(х)×H^T_¥(х)= H_¥(х)×G^T_¥(х) =0.

Для систематического ССК с алгоритмом порогового декодирования проверочная матрица H_¥ задается следующим образом:

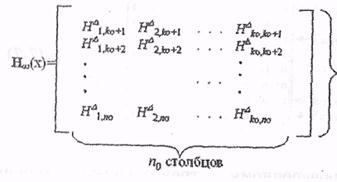
(n₀-k₀) строк

Из данной проверочной матрицы следует, что для ССК с 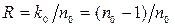проверочная матрица Н¥(х) содержит (n₀–k₀) строк и k₀ столбцов проверочных треугольников. Для ССК с 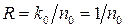, n₀ = 2;3; …, проверочная матрица Н¥(х) содержит k₀ =1, т.е. один столбец и n₀ строк проверочных треугольников.

Каждый из проверочных треугольников Н^D_i, _k0+i, i= 1,2, …; k₀= 1,2,…, проверочной матрицы Н_¥ (х) общем случае имеет вид:

,

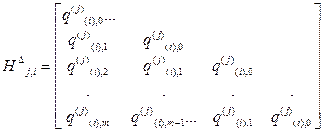где q – коэффициенты, равные либо 1, либо 0; j, i – номера соответственно строки и столбца матрицы Н _¥ (х), которыми определяется проверочный треугольник; 0, …m – порядковые номера степеней, в которые возводятся соответствующие коэффициенты порождающего полинома.

Основную информацию о самоортогональных сверточных кодах ССК несут коэффициенты левого столбца и нижней строки проверочного треугольника.

Пример: задан проверочный треугольник:

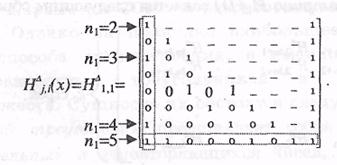
По данному проверочному треугольнику можно определить параметры ССК с алгоритмом ПД:

1. Поскольку задан один проверочный треугольник, то k₀= 1, n₀=k₀ +1=2,. 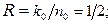r=(n₀-k₀)/n₀×100%=(1-R)×100%=50%.

2. Так как k₀ =1, то ССК задается одним порождающим полиномом, определяемым коэффициентами левого столбца и нижней строки проверочного треугольника.

g(x)=1+x²+x⁶+x⁷

3. Количество ненулевых членов порождающего полинома определяет число проверочных уравнений: J =4. Следовательно, ССК может исправлять 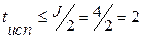ошибки и обнаруживать 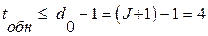ошибки.

d₀=J+1=4+1=5

4. Строки проверочного треугольника, которые начинаются с ненулевых двоичных символов, формируют проверочные уравнения, размеры данных проверок и номера позиций информационных и проверочных символов, участвующих в формировании проверочных уравнений. Размеры проверок в проверочном треугольнике обозначены цифрами перед стрелками и определяются количеством ненулевых символов в строке. Для данного примера имеем:

s₀=е₀ⁱ+e₀^p (i– информационный символ, р – проверочный)

s₂=е₀ⁱ+e₂ⁱ+e₂^p

s₆=е₀ⁱ+e₄ⁱ+e₆ⁱ+e₆^p

s₇=е₀ⁱ+e₁ⁱ+e₅ⁱ+e₇ⁱ+e₇^p

5. Длина кодового ограничения n_A и эффективная длина кодового ограничения n_e СК равны, соответственно,

n_A=(m+ 1 )n₀= (7+1)2=16 двоичных символов;

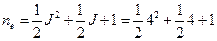=8+2+1=11 двоичных символов.

На практике наибольшее применение получили два способа построения проверочных треугольников:

- с помощью разностных треугольников

- с помощью совершенных разностных множеств.

III. Задание систематических СК с помощью разностных треугольников

Разностный треугольник представляет собой совокупность целых, действи­тель­ных и неповторяющихся чисел, записанных в форме треугольника. Для ССК с R = k₀/n₀ количество разностных треугольников равно числу k₀. Для всех разностных треугольников общим числом является “0”, который не указывается в совокупности чисел, однако учитывается при выборе степеней ненулевых членов порождающих полиномов. Степени ненулевых членов порождающих полиномов по заданным или построенным разностным тре­уголь­ни­кам можно найти путем выбора чисел:

· левого крайнего столбца разностного треугольника, считывая их сверху вниз и дополняя числом “0”,

· верхней строки разностного треугольника в такой последовательности: первое число – показатель степени второго ненулевого члена порождающего полинома; суммирование первого и второго чисел первой строки разностного треугольника определяет показатель степени третьего ненулевого члена порождающего полинома и т.д.

Пример: Определить параметры ССК с алгоритмом ПД при следующем разностном треугольнике:

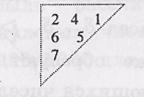
1. Так как задан один разностный треугольник, то k₀= 1, n₀=k₀ +1=2, 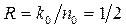, код имеет один порождающий полином.

2. Выписывая числа левого крайнего столбца разностного треугольника, определяем показатели степеней порождающего полинома: (0,2,6,7). Следо­ва­тель­но, порождающий полином ССК имеет вид: g(х)= 1 +x²+x⁶+x⁷. При втором способе –0; 2; 2+4=6; 2+4+1=7. Как правило, в литературе разностные треугольники табулированы и представлены, например, так: ((2,4,1), (3,5,2)). Это означает, что ССК имеет соответственно параметры: k₀ =2, n₀=k₀ +1=3, 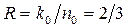и g₁(x)=1+x²+x⁶+x⁷ и g₂(x)=1+x³+x⁸+x¹⁰.

Разностный треугольник ССК может быть построен, если задан прове­роч­ный треугольник, и наоборот.

Пример: По проверочному треугольнику построить разностный.

Числа крайнего левого столбца разностного треугольника определяются как результат операции вычитания порядковых номеров строк проверочного треугольника, которые начинаются с “1”. Для первого столбца получаем следующие числа: 3–1=2 (3 – номер позиции третьей строки, 1 – номер позиции первой строки); 7–1=6 и 8–1=7. Для получения чисел второго столбца за вычитаемое берем номер позиции третьей строки: 7–3=4 и 8–3=5. Для получения чисел третьего столбца за вычитаемое берем номер позиции седьмой строки: 8–7=1.

Числа, входящие в разностные треугольники, должны быть целыми, действительными и неповторяющимися. Только в этом случае будет сформирована система ортогональных (раздельных) проверок. Для получения совокупности таких чисел известно достаточно много способов их нахождения, но наиболее эффективным является способ, основанный на теории совершенных разностных множеств.

V. Задание систематических СК с использованием

совершенных разностных множеств

Совершенное разностное множество – это совокупность целых, дей­стви­тель­ных и неповторяющихся чисел d₁, d₂, … d_x, причем d₁<d₂<d_x и разности этих чисел 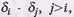полученных по некоторому mod x (x¹2), также образующих совокупность целых, действительных и неповторяющихся чисел.

Данную совокупность полученных разностных чисел можно использовать в качестве исходных чисел для формирования разностных треугольников и выбора соответствующих порождающих полиномов ССК.

При выборе чисел для построения разностных треугольников необходимо выбирать числа с наименьшим их значением по номиналу, т.к. максимальное значение числа в построенных разностных треугольниках определяет максимальную степень m порождающих полиномов ССК.

Рассмотрим построение ССК с алгоритмом ПД с использованием совер­шен­ных разностных множеств.

Пусть, например, имеется совокупность b= 3-х целых, действительных и неповторяющихся чисел (b= 1,2,3) и эта совокупность образует b²+b= 3²+3=12разностей по модулю b ² +b+ 1 = 3²+3+1=13, которые равны следующим числам:

1 – 0º1	12 – 8º4	2 – 8º7	0 – 3º1
3 – 1º2	0 – 8º5	8 – 0º8	1 – 3º11
3 – 0º3	8 – 2º6	8 – 12º9	0 – 1º12

Полученную совокупность разностных чисел можно разбить на следующие подмножества:

1

.

	j

Каждый из столбцов данного множества можно использовать для построения разностного треугольника. Следовательно, можно построить k₀=4 разностных треугольника и четыре ССК с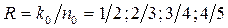, с J =4 и с 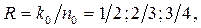с J= 5, разбив данное множество на три подмножества.

Отметим, что с использованием теории совершенных разностных множеств были рассчитаны и табулированы показатели степеней ненулевых членов порождающих полиномов ССК с 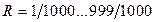для J =2…16.

Рассмотрим кодирование информации на примере систематического ССК с R=1/2 и корректирующего двойные ошибки (t_испр=2 дв.симв.). Для ССК, как и для блочных циклических кодов, структура кодера полностью определяется порождающим полиномом g(x) и реализуется с помощью линейных автоматов без обратной связи с вынесенными или встроенными сумматорами по модулю два.

Для ССК, корректирующего двойные ошибки, достаточно использовать один по­рождающий полином вида g(x)=1+x²+x⁵+x⁶, у которого имеется J=2×t _испр=2*2=4 орто­го­наль­ных проверок и соответственно столько же ненулевых членов. Данный ССК исправ­ляет двукратные ошибки на длине кодового ограничения, равного n_А=(m+ 1 )×n₀= (6+1)×2=14 символам. Отметим, что для высокоскоростных ССК (R ³ 2/3) в кодере целесообразно использовать линейные автоматы со встроенными сумматорами по модулю два; в теории СК его называют кодером Месси.

На рис. 2 и 3 приведены кодеры со встроенными и вынесенными сумматорами по модулю два для данного кода.

Рис. 2. Кодер ССК со встроенными сумматорами по модулю два

Рис. 3. Кодер ССК с вынесенными сумматорами по модулю два

Для дальнейшего анализа алгоритмов кодирования и декодирования ССК используем обобщенную структурную схему кодера ССК, пред­став­лен­ную на рис. 4.

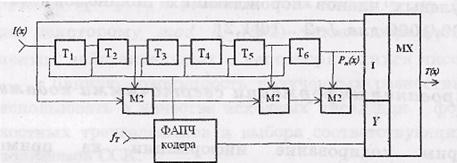
Рис. 4. Обобщенная структурная схема кодера ССК

Т. к. кодер ССК формирует два синхронных потока (n₀= 2) кодовых символов, для получения единого потока можно использовать синхронный мультиплексор (МХ). Управление работой блока кодера и муль­ти­­плексора осуществляется блоком фазовой автоподстройки частоты (ФАПЧ).

Кодирование информации ССК осуществляется следующим образом. Входная информационная последовательность I(x) одновременно поступает на вход мультиплексора и блока кодирования, на выходе которого фор­ми­ру­ют­ся проверочные символы Р(х), которые поступают на второй инфор­ма­ци­он­ный вход мультиплексора.

Выходная кодовая последовательность Тⁱ(х) и входная информационная последовательность I^j(х)связаны выражением:

.

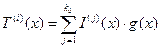Каждый входной информационный символ оказывает влияние на формирование кодовой последовательности в течение (m+1)=(6+1)=7 тактов, и, следовательно, с выхода кодера будет считано n_А=(m+1)×n₀=7×2=14 кодовых символа. Отсюда видно, что данный процесс кодирования СК осуществляется с памятью в отличие от циклических кодов.

С выхода кодера ССК символы кодовой последовательности Т(х) поступают на вход модулятора, где преобразуются в аналоговый сигнал и далее передаются по каналу связи. Данный способ кодирования получил название прямого (непосредственного) способа кодирования информации. Этот способ требует небольших затрат на кодирование информации, что связано с использованием минимального объема оборудования.

При независимом кодировании нечетных и четных информационных символов СК информация от источника поступает на вход коммутатора распределения информации (КРИ), где распределяется на два потока: I₁(x)– поток нечетных информационных символов, I₂(x) – поток четных информационных символов. Двоичные символы данных потоков кодируются независимо друг от друга СК и поступают на соответствующие входы модулятора и далее передаются в канал связи. К достоинствам данного способа кодирования следует отнести: возможность выбора СК с меньшей избыточностью и, сле­до­ва­тельно, с меньшей сложностью реализации кодеков. К недостаткам отно­сится двукратное увеличение объема оборудования и сложность реализации устройств ветвевой синхронизации распределителей информации кодеков.

При прямом кодировании информации с перемежением кодовых символов обеспечивается коррекция группирующихся ошибок кодами, корректирующими независимые ошибки. К недостаткам данного способа кодирования относятся: увели­чение задержки информации при декодировании и сложность реали­за­ции устройств ветвевой синхронизации распределителей информации кодека СК.

Используется также способ каскадного кодирования информации СК (рис. 5).

Рис. 5. Способ каскадного кодирования информации СК

В этом случае информационные символы I(x) первоначально кодируются внешним кодером, используемым для коррекции пакетных ошибок определенной кратности, а затем кодовые символы последовательности Т ₁ (x) кодируются внутренним кодером, рассчитанным для коррекции независимых ошибок. С выхода внутреннего кодера кодовые символы последовательности Т ₂ (x) посту­па­ют на вход модулятора и далее в канал. С целью повышения корректирующей способности к группирующимся ошибкам возможно дополнительное перемежевание кодовых символов либо после внешнего кодера, либо после внутреннего кодера.

Достоинством данного способа кодирования является возможность одновременной коррекции как пакетных, так и независимых ошибок, защита информации от несанкционированного доступа при использовании во внутреннем кодере несистематических СК. Недостатком системы является высокая избыточность каскадного кода и большая задержка информации при декодировании.

Структурная схема кодера

КРИ-1/k₀ – коммутатор распределения информации;

ФПС_кодера – формирователь проверочных символов кодера;

КОИ-n₀/1 – коммутатор объединения информации.