Каскадные коды: определение, принцип построения, основные характеристики

Реальные каналы связи, особенно каналы связи на основе стандартных каналов тональной частоты, являются каналами связи с группированием ошибок, причем длина пакетов ошибок может находиться в пределах от десятков двоичных символов до нескольких сотен двоичных символов. Кроме того, в защитных интервалах между пакетами ошибок имеются случайные ошибки. Для коррекции ошибок такой структуры требуются мощные помехоустойчивые коды, а это значит, необходимо использовать помехоустойчивые коды с очень большой длиной кодовых последовательностей и с высокой, избыточностью. Такие коды обладают высокой сложностью реализации и большой задержкой информации при декодировании.

Для коррекции ошибок данной структуры был разработан способ кодирования информации, который обеспечивает требуе­мую верность передачи информации при меньшей сложности реализации кодека и задержки информации при декодировании. Сущность данного способа кодирования информации состоит в каскадировании двух или более кодов, т.е. в использовании нескольких уровней или ступеней кодирования и декодирования информации. При этом на каждом уровне кодирования могут использоваться либо одинаковые по типу и корректирующей способности коды, либо разные.

Наиболее распространенной схемой построения каскадных кодов является двухкаскадная или двухступенчатая схема:

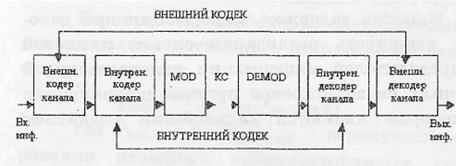
В качестве внешнего кода чаще всего используются коды Рида-Соломона, корректирующие пакетные ошибки, а внутрен­ним кодом могут быть различные циклические и сверточные коды, корректирующие случайные ошибки. В реальных систе­мах связи в качестве внутреннего кода используются сверточные коды с алгоритмом декодирования Витерби.

Кодирование и декодирование информации производится следующим образом. Во внешнем кодере передаваемая информация кодируется кодом, рассчитанным для коррекции пакетных ошибок. Чаще всего используются недвоичные коды Рида-Соломона. Далее символы кодовых последовательностей внешнего кода кодируются внутренним кодом. С выхода внутреннего кодера кодовые символы каскадного кода поступают на вход модулятора и далее передаются в канал связи. На приемной стороне первоначально производится обработка информации внутренним декодером, а затем внешним декодером. С целью повышения корректирую­щей способности внутреннего кода к выходу внутреннего кодера подключается перемежитель кодовых символов. Сущность перемежения кодов состоит в рассредоточении ошибок, входящих в пакет по различным кодовым словам кодов, исправляющих случайные ошибки.

Достоинством каскадных кодов является высокая коррек­тирующая способность, а недостатком является высокая избыточность информации. С целью уменьшения избыточности каскадного кода в качестве внутреннего кода используются высокоскоростные (малоизбыточные) сверточные коды.

Сверточные коды: определение, параметры, классификация

Сверточные коды (СК) имеют большой научный и практический интерес для современных систем и сетей телекоммуникаций. Это определяется многими их достоинствами, а именно:

1. высокой скоростью обработки информации (десятки и сотни Мбит/с),

2. высокой корректирующей способностью как случайных, так пакетных ошибок,

3. реализацией эффективных кодеков,

4. эффективным применением в каналах связи с фазовой неопределенностью и др.

В общем виде кодирование информации СК может быть представлено следующим образом:

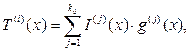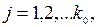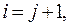(1)

где I(x) – последовательность передаваемых информационных символов; x – формальная переменная; g(x) – порождающий, или образующий, полином (многочлен); k₀ – блок информационных символов, одновременно поступающих на вход кодирующего устройства (k₀).

Способ формирования кодовых символов, выполняемых согласно (1), соответствует форме записи свертки двух функций, что и послужило названию данных кодов. Сверточный код – это рекуррентный код (т.е. операции выполняются шаг за шагом) с периодической полубесконечной структурой символов кодовой последовательности. Обобщенная структурная схема кодера СК представлена на рис. 1.

Рис. 1. Обобщенная структура кодера СК

Входные информационные символы I(x) делятся на k₀ символов, которые одновременно с каждым тактом поступают на входы кодера СК, в котором согласно (1) формируются кодовые символы n₀. Таким образом, кодовая последовательность Т⁽ⁱ⁾(x) представляет собой полубесконечную последовательность блоков n₀.

Существенное отличие СК от ЛБК: для ЛБК проверочные символы зависят от одного информационного блока, а для СК проверочные символы зависят как от информационных символов на входе, так и от некоторого количества предшествующих.

Любому входному информационному блоку из k₀ информационных символов и m предшествующих символов, хранящихся в регистре сдвига кодера, соответствует выходной кодовый миниблок из n₀ двоичных символов. Т.к. в алгоритме кодирования участвуют предшествующие символы m, то такой алгоритм называется кодирование с памятью.

К основным параметрам СК относятся:

1. 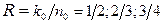и т.д. – скорость передачи кода, которая для СК записывается в виде дроби;

2. l=n₀-k₀ – абсолютная избыточность;

3. r=(n₀-k₀)/n₀×100%=(1-R)×100% – относительная избыточность;

4. J≥2 – количество ортогональных проверочных уравнений, т.е. количество ненулевых членов в образующем полиноме;

5. d₀=J+1 – минимальное кодовое расстояние;

6. 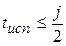– кратность или количество исправляемых ошибок;

7. – кратность обнаруживаемых ошибок;

8. n_A=(m+1)n₀ – длина кодового ограничения, или длина кодовой последовательности, соответствующая кодированию информационных блоков из k₀ символов в течение (m+ 1) такта; m – старшая степень ненулевого многочлена порождающего полинома;

9. k_A=R×n_A – количество информационных символов, приходящихся на n_A кодовых символов;

10. n_E=J²/2+J/2+1 –эффективная длина кодового ограничения (количество двоичных символов, непосредственно участвующих в декодировании).

Классификация СК.

- По основанию кода: двоичные и недвоичные;

- В зависимости от используемого математического аппарата: алгебраические и неалгебраические;

- По алгоритму формирования проверочных символов: линейные и нелинейные;

- По способу передачи: систематические и несистематические;

- По структуре кодовой последовательности: разделимые и неразделимые;

- По алгоритму декодирования: ортогональные и неортогональные;

- По способу преобразования входных информационных символов k₀ в кодовые символы СК являются непрерывными.

В зависимости от способа формирования проверочных уравнений СК бывают ортогональными, самоортогональными и ортогонализируемыми.

Ортогональными СК (ОСК) называют такие коды, в которых система из J (J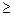2) проверочных уравнений ортогональна относительно декодируемых k₀ информационных символов и неортогональна относительно информа­цион­ных символов, входящих в данные проверочные уравнения.

Самоортогональные СК (ССК) – коды, в которых декодируемый инфор­ма­ци­он­ный символ входит одновременно во все проверочные уравнения, а все осталь­ные символы, участвующие в декодировании в данный момент времени, входят не более, чем в одно проверочное уравнение, т.е. СК формирует так называемую, систему раздельных проверок.

Ортогонализируемыми СК называются такие коды, у которых при деко­ди­ро­ва­нии информационного или k₀ символов требуется выполнить допол­ни­тель­ные линейные преобразования над проверочными символами для получения дополнительных, так называемых составных проверок.