Снятие условия полной независимости процесса приращений цен приводит к третьей версии ГСБ - ГСБ-3, согласно которой автокорреляционные связи между приростами отсутствуют, однако автокорреляция между их степенями может иметь место.
.
Существуют по крайней мере две причины, по которым финансовая эконометрика часто отдает предпочтение временным рядам доходов по сравнению с рядами цен. Во-первых, есть основание предполагать, что для инвесторов финансовые рынки представляются достаточно совершенными механизмами в том смысле, что уровень цен на них не зависит от размера инвестиций. В такой ситуации привлекательность вложений капитала не зависит от вида товара и вследствие этого определяется величиной дохода, а не уровнем его цены. Во-вторых, свойства временных рядов доходов, как правило, предпочтительнее с точки зрения статистики. Им, например, в большей мере присуща стационарность, чем рядам цен.
Однако взаимосвязи между однопериодными доходами и доходом за объединенный период, выраженные произведением, также не очень удобны с точки зрения статистического анализа. В частности, усредненный за 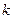 периодов доход в этом случае рассчитывается как среднегеометрическое значение.
периодов доход в этом случае рассчитывается как среднегеометрическое значение.
Вместе с тем математическая статистика и эконометрика в большей степени оперирует среднеарифметическими показателями. Такую возможность представляет использование логарифмов доходов, которые называют «непрерывно составными доходами».
Различные классы моделей финансовой эконометрики базируются на характерных для наблюдаемого временного ряда определенного финансового показателя, в качестве которого могут выступать непосредственно цены, доходы (чистые, валовые, логарифмические), а также их приросты, ошибки моделей и некоторые другие характеристики. Примером этих характеристик могут являться также и функциональные преобразования финансовых показателей, например, линейные и степенные функции от них. Значительная часть таких взаимосвязей может быть определена общим выражением, означающим отсутствие автоковариационных связей между временными рядами, образованными различными функциональными преобразованиями рассматриваемого финансового показателя, следующего вида:
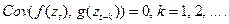
В этом выражении в качестве аргумента 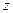 функций
функций 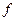 и
и 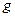 выступает одна из перечисленных выше характеристик финансового показателя (цена, какая-либо из ее производных, функция от цены или ее производной и т.п.), рассматриваемая в моменты t и
выступает одна из перечисленных выше характеристик финансового показателя (цена, какая-либо из ее производных, функция от цены или ее производной и т.п.), рассматриваемая в моменты t и 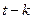 соответственно. Данное выражение часто называют ортогональным условием. Различные сочетания входящих в него функций соответствуют вполне определенным предпосылкам относительно характера взаимосвязей во временном ряду финансового показателя (исходные гипотезы), которые и кладутся в основу описывающей этот ряд модели. Рассмотрим некоторыеизнаиболее известных предпосылок более подробно.
соответственно. Данное выражение часто называют ортогональным условием. Различные сочетания входящих в него функций соответствуют вполне определенным предпосылкам относительно характера взаимосвязей во временном ряду финансового показателя (исходные гипотезы), которые и кладутся в основу описывающей этот ряд модели. Рассмотрим некоторыеизнаиболее известных предпосылок более подробно.
Одна из самых «старых» гипотез относительно взаимосвязей во временном ряду цен, лежащая в основе так называемой «мартингальной модели», предполагает отсутствие автокорреляционных взаимосвязей между приростом цен при любых сдвигах.
Случайный процесс 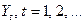 , характеризующий динамику цены в этом случае удовлетворяет следующему условию:
, характеризующий динамику цены в этом случае удовлетворяет следующему условию:
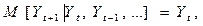
которое эквивалентно соответствующему условию для приростов цен
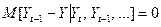
Последние выражения свидетельствуют о том, что условное математическое ожидание цены в момент 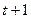 при известных ее значениях в периоды времени
при известных ее значениях в периоды времени 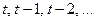 равно ее значению в момент
равно ее значению в момент 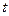 , которое, в свою очередь, предопределено предшествующей динамикой этой цены или, что эквивалентно, условное математическое ожидание прироста цены за интервал
, которое, в свою очередь, предопределено предшествующей динамикой этой цены или, что эквивалентно, условное математическое ожидание прироста цены за интервал 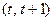 при известной ее предыстории равно нулю и, таким образом, прирост цены не зависит от предшествующих уровней цен. Последнее допущение также означает, что любые (по величине лага) не пересекающиеся во времени приросты цен некоррелированы между собой, что предопределяет невозможность их предсказания с помощью линейных моделей временных рядов. Таким образом, «лучший прогноз» цены на дату
при известной ее предыстории равно нулю и, таким образом, прирост цены не зависит от предшествующих уровней цен. Последнее допущение также означает, что любые (по величине лага) не пересекающиеся во времени приросты цен некоррелированы между собой, что предопределяет невозможность их предсказания с помощью линейных моделей временных рядов. Таким образом, «лучший прогноз» цены на дату 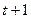 - это ее уровень на дату
- это ее уровень на дату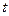 .
.
Последние условия удовлетворяют предпосылкам так называемого «эффективного рынка», одна из важнейших среди которых свидетельствует о том, что текущая цена полностью предопределена информацией, содержащейся в ценах предыдущих периодов и не существует никакой другой информации, поступившей в период (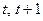 ), эксклюзивное владение которой позволяет участникам торговых сделок извлечь дополнительную прибыль. Следовательно, условное математическое ожидание прироста цены на ее предшествующие значения не может быть ни положительным, ни отрицательным, «обязано» быть равным нулю, и изменения цены являются абсолютно случайными и непредсказуемыми.
), эксклюзивное владение которой позволяет участникам торговых сделок извлечь дополнительную прибыль. Следовательно, условное математическое ожидание прироста цены на ее предшествующие значения не может быть ни положительным, ни отрицательным, «обязано» быть равным нулю, и изменения цены являются абсолютно случайными и непредсказуемыми.
С точки зрения «ортогонального» условия предпосылки мартингальной модели означают, что функция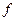 является линейной с аргументом, выражающим прирост цен в текущем периоде, а функция
является линейной с аргументом, выражающим прирост цен в текущем периоде, а функция 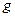 может быть любой по отношению к этому аргументу, рассматриваемому в предшествующие периоды. Кроме линейной функции прироста качестве
может быть любой по отношению к этому аргументу, рассматриваемому в предшествующие периоды. Кроме линейной функции прироста качестве 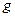 может рассматриваться, например, любая степенней функция от этого аргумента, т.е.
может рассматриваться, например, любая степенней функция от этого аргумента, т.е.
Достаточно широкий класс моделей финансовой эконометрики базируется на предположении о том, что приросты цен эквивалентны случайному процессу по своим свойствам близкому к «белому шуму». Это предположение отражает сущность так называемой «гипотезы случайного блуждания» (ГСБ). В научной литературе описаны три версии этой гипотезы, которые отличаются друг от друга содержанием, вкладываемым в понятие «белого шума». Согласно первой версии этой гипотезы - ГСБ-1, разработанной еще в начале XX века, — случайные приросты финансового показателя (цены) и любые их функциональные преобразования независимы и удовлетворяют условию стационарности или, иначе, имеют идентичные условные распределения на уровни цен в прошедшие моменты времени. Таким образом, ГСБ-1 утверждает, что динамика приростов цены по своим свойствам соответствует процессу «строгого белого шума». Как правило, закон распределения приростов предполагается нормальным, в специальных случаях - стабильным. Отказ от идентичности закона распределения приростов является логичным развитием ГСБ-1, «смягчающим» ее достаточно строгие ограничения в отношении свойств приростов цены.
Предположение о независимости приростов цены и неидентичности их условных распределений выражает сущность второй версии ГСБ - ГСБ-2. В частном случае ГСБ-2 допускает случайные измерения значений рассматриваемого ряда. ГСБ-2, как ГСБ-1, предполагает, что как сами приросты, так и любые их функции независимы между собой. Они могут быть как линейными, так и степенными. ГСБ-2 была обоснована уже во второй половине XX века.
(4 часа)
Прогнозирование одна из основных сфер практического применения эконометрических моделей. Эконометрические прогнозные исследования, начало которым было положено в конце 20-х годов XX столетия, уже через два-три десятилетия сформировались в самостоятельное направление в экономической науке. Попытки разработки прогнозов финансовых показателей на основе простейших типов моделей финансовой эконометрики предпринимались фактически с момента формирования финансовых рынков. Круг прогнозируемых процессов постоянно расширялся. В настоящее время эконометрические прогнозы разрабатываются практически для всех процессов, характеризующих развитие общества как на микро-, так и на мезо-, и макроуровнях его организации. Самое широкое применение эконометрические модели находят в разработках прогнозов спроса и предложения, научно-технического прогресса, финансов и цен, уровня жизни, производительности труда, валового продукта, миграции, занятости и многих других явлений.
Термин «эконометрическое прогнозирование» обычно означает процедуру получения на основе эконометрических моделей некоторых характеристик зависимого процесса у (совокупности зависимых процессов), относящихся к следующим за моментом 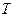 (последней точкой периода наблюдения) моментам
(последней точкой периода наблюдения) моментам 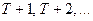 . Для «типовой» эконометрической модели, состоящей из единственного уравнения, к числу важнейших таких характеристик относятся непосредственно прогнозные значения зависимой переменной
. Для «типовой» эконометрической модели, состоящей из единственного уравнения, к числу важнейших таких характеристик относятся непосредственно прогнозные значения зависимой переменной 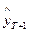 ,
, 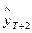 ,… (точечные прогнозы) и показатели их точности - обычно дисперсии прогнозов
,… (точечные прогнозы) и показатели их точности - обычно дисперсии прогнозов  ,
,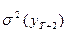 …, доверительные интервалы, в которых с заданной вероятностью будут находиться «истинные» значения рассматриваемого процесса
…, доверительные интервалы, в которых с заданной вероятностью будут находиться «истинные» значения рассматриваемого процесса 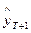 ,
, 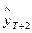 ,…(интервальные прогнозы).
,…(интервальные прогнозы).
В этой связи следует отметить, что развитие эконометрических прогнозных исследований в значительной степени было обусловлено именно относительной простотой процедур разработки прогнозов, ясностью и определенностью использования их результатов в практике управления общественным развитием. В самом деле, для построенной на интервале времени (1,Т) эконометрической модели 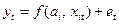 , с известными оценками коэффициентов
, с известными оценками коэффициентов 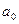 и
и 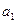 , … процедура определения точечных прогнозов
, … процедура определения точечных прогнозов 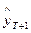 ,
, 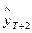 ,… сводится к подставлению в уравнение модели соответствующих прогнозным моментам Т+1, Т+2,... значений независимых переменных
,… сводится к подставлению в уравнение модели соответствующих прогнозным моментам Т+1, Т+2,... значений независимых переменных 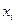 , i =1, 2,..., п; и фактической ошибки
, i =1, 2,..., п; и фактической ошибки 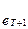 ,
, 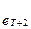 ,…Заметим, что для «типовой» линейной модели
,…Заметим, что для «типовой» линейной модели 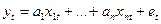 для получения точечного прогноза
для получения точечного прогноза 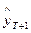 в ее уравнение необходимо подставить значения независимых переменных
в ее уравнение необходимо подставить значения независимых переменных 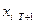 , i =1, 2,..., п; выражающих их уровни в этот же момент Т+1. В некоторых исследованиях, когда момент Т+1 относится к «будущему», эти уровни могут быть точно не известными. Они могут определяться по результатам других прогнозных разработок, отражать какие-либо гипотезы, выдвигаемые в отношении характера развития независимых переменных. Если ошибка модели удовлетворяет стандартным для нее предположениям (равенство нулю математического ожидания, отсутствие автокорреляционных связей и т.д.), то точечный прогноз в этом случае определяется как оценка математического ожидания значения у в точке Т+1 в предположении, что оценки коэффициентов
, i =1, 2,..., п; выражающих их уровни в этот же момент Т+1. В некоторых исследованиях, когда момент Т+1 относится к «будущему», эти уровни могут быть точно не известными. Они могут определяться по результатам других прогнозных разработок, отражать какие-либо гипотезы, выдвигаемые в отношении характера развития независимых переменных. Если ошибка модели удовлетворяет стандартным для нее предположениям (равенство нулю математического ожидания, отсутствие автокорреляционных связей и т.д.), то точечный прогноз в этом случае определяется как оценка математического ожидания значения у в точке Т+1 в предположении, что оценки коэффициентов 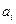 и уровни факторов
и уровни факторов 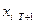 независимы, i =1,2,..., п.
независимы, i =1,2,..., п.
Вместе с тем следует иметь в виду, что «высокое качество» прогнозной эконометрической модели не является достаточной гарантией обоснованности эконометрических прогнозов, особенно в отдаленной перспективе. Дело в том, что в будущем тенденции развития рассматриваемых процессов, структура и сила взаимосвязей между ними могут существенно изменяться. Эти изменения могут носить эволюционный характер, накапливаясь постепенно, например, вследствие роста масштабов явлений. Они могут происходить и скачкообразно вслед за финансовыми кризисами, революционными преобразованиями в обществе и т.п. При этом «удачная» для периода (1,Т) эконометрическая модель, как правило, не сможет учесть такие изменения, поскольку она построена на основе информации, отражающей иной характер взаимосвязей между рассматриваемыми явлениями, имевший место в прошлом. В некоторых случаях обоснованность и достоверность эконометрических прогнозов могут быть повышены путем либо корректировки самих результатов формальной экстраполяции, т.е. «предварительных» прогнозных значений 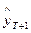 ,
, 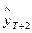 ,…, полученных непосредственно с использованием построенной эконометрической модели, либо предварительной (до прогноза) корректировки самой модели, исходя из некоторых дополнительных сведений, предположений. Зачастую такие корректировки осуществляются на основе экспертной информации. В отношении этого американский экономист П. Самуэльсон заметил: «...почти все эконометрики, за редким исключением, корректируют параметры моделей с помощью неформальных методов, считая, что это улучшает результат». Обосновывая необходимость уточнения «формальных» эконометрических прогнозов, другой американский экономист М. Уитмент пишет: «Использование эконометрических моделей позволяет опереться на критерии точных дисциплин и получить внутренне согласованные прогнозы. Однако сырые результаты модельных расчетов, так же как и их основополагающие предпосылки, должны быть подвергнуты тщательному экспертному анализу».
,…, полученных непосредственно с использованием построенной эконометрической модели, либо предварительной (до прогноза) корректировки самой модели, исходя из некоторых дополнительных сведений, предположений. Зачастую такие корректировки осуществляются на основе экспертной информации. В отношении этого американский экономист П. Самуэльсон заметил: «...почти все эконометрики, за редким исключением, корректируют параметры моделей с помощью неформальных методов, считая, что это улучшает результат». Обосновывая необходимость уточнения «формальных» эконометрических прогнозов, другой американский экономист М. Уитмент пишет: «Использование эконометрических моделей позволяет опереться на критерии точных дисциплин и получить внутренне согласованные прогнозы. Однако сырые результаты модельных расчетов, так же как и их основополагающие предпосылки, должны быть подвергнуты тщательному экспертному анализу».
В такой ситуации при эконометрическом прогнозировании уместным является вопрос о максимально возможной глубине прогнозного периода. Однозначного ответа на него дать невозможно. Очевидно, что чем более инерционным является рассматриваемый процесс, чем устойчивее его взаимосвязи, чем стабильнее ситуация в обществе, экономике, тем больше может быть и прогнозный период. В некоторых научных публикациях можно встретить рекомендации определять глубину эконометрического прогноза как 1/3 или 1/2 от величины оценочного периода, т.е. как 1/3 Т, 1/2 Т. Обзор эконометрических прогнозных исследований свидетельствует, что многофакторные эконометрические модели, как правило, используются при разработке так называемых краткосрочных, и в крайнем случае, среднесрочных прогнозов. Для многих реальных социально-экономических процессов (спрос, производительность труда, выпуск продукции и т.п.) такие прогнозы разрабатываются на 5-10 временных точек (кварталов, лет - в зависимости от длины интервала 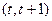 ). Эти рекомендации не относятся к прогнозам финансовых показателей, которые разрабатываются на основе моделей финансовой эконометрики. «Финансовые» прогнозы являются, как правило, краткосрочными (на один, два шага вперед), в то время как модели финансовой эконометрики формируются на основе достаточно длинных временных рядов исходных данных. Это связано с тем, что практически всегда имеется возможность получить «свежую» информацию о текущем уровне рассматриваемого процесса (данные с финансовых рынков становятся доступными без задержки), и на ее основе скорректировать построенную модель. Достаточно очевидны и выводы, следствия, которые могут быть получены из эконометрических прогнозов, например в сфере управления. В этой связи заметим, что эконометрические прогнозы разрабатываются для оценки будущих состояний рассматриваемого процесса в зависимости от ожидаемых уровней влияющих на него факторов. При этом, в общем случае факторы можно разделить на три группы: управляемые, неуправляемые и частично управляемые.
). Эти рекомендации не относятся к прогнозам финансовых показателей, которые разрабатываются на основе моделей финансовой эконометрики. «Финансовые» прогнозы являются, как правило, краткосрочными (на один, два шага вперед), в то время как модели финансовой эконометрики формируются на основе достаточно длинных временных рядов исходных данных. Это связано с тем, что практически всегда имеется возможность получить «свежую» информацию о текущем уровне рассматриваемого процесса (данные с финансовых рынков становятся доступными без задержки), и на ее основе скорректировать построенную модель. Достаточно очевидны и выводы, следствия, которые могут быть получены из эконометрических прогнозов, например в сфере управления. В этой связи заметим, что эконометрические прогнозы разрабатываются для оценки будущих состояний рассматриваемого процесса в зависимости от ожидаемых уровней влияющих на него факторов. При этом, в общем случае факторы можно разделить на три группы: управляемые, неуправляемые и частично управляемые.
Если прогноз разрабатывается на основе неуправляемых факторов (погодные условия, состояние мировой экономики и т.п.), то и сам процесс является неуправляемым. Прогнозы таких процессов часто называют поисковыми (исследовательскими). В этом случае система управления имеет возможность только приспособиться к его тенденциям прогнозируемого процесса, учесть их при обосновании управляющих мер для соответствующего объекта. Если факторы являются управляемыми, то система управления может сознательно выбирать, формировать их уровни, определяя тем самым наиболее рациональную, «оптимальную» для объекта тенденцию развития процесса в прогнозном периоде. Такие прогнозы обычно называют нормативными. При частично управляемых факторах возможности регулирования развития процесса в прогнозный период являются ограниченными. Например, из-за того, что в моделях присутствуют факторы обеих групп. Часто эти ограничения обусловлены имеющимися ресурсами (финансовыми, трудовыми, сырьевыми и т.п.).
В случае управляемых и частично управляемых факторов заметим, что эконометрические модели предоставляют исследователю фактически всю информацию относительно границ управления (диапазонов изменения факторов), эффективности их использования в управлении. При этом показатель эффективности в некоторой степени может быть определен на основании значений коэффициентов эластичности переменной у по факторам хi (в части определения реакции у на изменения хi). Другие составляющие эффективности (стоимость затрат на реализацию управления, результаты, выгоды, к которым оно приводит) выявляются на основе экономического анализа рассматриваемой проблемы.
В связи с проблемой управления также заметим, что эконометрические модели достаточно часто используются в разработках так называемых «прогнозов-предупреждений». Результаты таких прогнозов являются нежелательными для объекта, и реакция системы управления в этом случае состоит в определении мер, способных внести необходимые коррективы в тенденции развития процесса у, в рассматриваемый период. Эти меры в данном случае выражаются в виде необходимых приростов независимых управляемых факторов.
Одной из важнейших характеристик качества прогноза является величина его доверительного интервала. Очевидно, что при прочих равных условиях чем уже этот интервал, тем более обоснованным представляется и сам прогноз, и мероприятия по управлению рассматриваемым процессом.
В общем случае можно указать на два взаимодополняющих подхода к оценке доверительного интервала прогноза - эвристический и формальный. По своей сути эвристический подход предполагает расчет размера доверительного интервала как разницы между двумя возможными «экстремальными» значениями прогнозов переменной у полученными при подстановке в уравнение эконометрической модели определяющих их «экстремальных» значений факторов. Часто такие значения и соответствующие им прогнозы называют «пессимистическим» и «оптимистическим»:
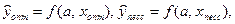
где 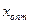 и
и 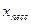 - оптимистические и пессимистические значения независимых факторов. Тогда ширина доверительного интервала прогноза определяется как разность
- оптимистические и пессимистические значения независимых факторов. Тогда ширина доверительного интервала прогноза определяется как разность 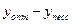 . Заметим, что рассчитанный таким образом «эвристический» доверительный интервал в большей степени характеризует возможный разброс прогнозируемого значения процесса в зависимости от разброса прогнозного фона, в свою очередь вызванного неопределенностью оценок его значений в перспективе. Формальный подход к оценке ширины доверительного интервала прогноза предполагает расчет этой характеристики с использованием методов математической статистики. Для этого необходимо оценить дисперсию ошибки прогноза.
. Заметим, что рассчитанный таким образом «эвристический» доверительный интервал в большей степени характеризует возможный разброс прогнозируемого значения процесса в зависимости от разброса прогнозного фона, в свою очередь вызванного неопределенностью оценок его значений в перспективе. Формальный подход к оценке ширины доверительного интервала прогноза предполагает расчет этой характеристики с использованием методов математической статистики. Для этого необходимо оценить дисперсию ошибки прогноза.
В общем случае ошибка эконометрического прогноза может быть определена как разность между фактическим значением рассматриваемого показателя 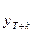 в некоторый момент времени
в некоторый момент времени 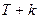 в будущем, которое, вообще говоря, неизвестно, и его значением
в будущем, которое, вообще говоря, неизвестно, и его значением 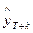 , k = 1,2,…:
, k = 1,2,…:  . При этом предполагается, что ошибка прогноза обладает следующими двумя свойствами: 1) несмещенности, что означает, что прогноз
. При этом предполагается, что ошибка прогноза обладает следующими двумя свойствами: 1) несмещенности, что означает, что прогноз 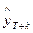 является несмещенной оценкой истинного значения
является несмещенной оценкой истинного значения 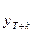 ; 2) эффективности, т.е. дисперсия ошибки является минимальной среди дисперсий всех других возможных прогнозов, построенных с использованием данного эконометрического уравнения.
; 2) эффективности, т.е. дисперсия ошибки является минимальной среди дисперсий всех других возможных прогнозов, построенных с использованием данного эконометрического уравнения.
Далее, в предположении, что ошибка прогноза распределена согласно закону нормального распределения, доверительный интервал для истинного значения прогноза может быть определен согласно следующему известному выражению:
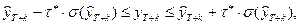
где 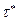 - табличная константа, полученная для стандартизованного нормального распределения N(0,1) при заданном уровне доверительной вероятности
- табличная константа, полученная для стандартизованного нормального распределения N(0,1) при заданном уровне доверительной вероятности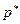 . Напомним, например, для
. Напомним, например, для 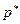 =0,95
=0,95 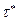 =1,96.
=1,96.
Таким образом, при определении ширины доверительного интервала эконометрического прогноза с использованием формального подхода основной проблемой является оценка дисперсии рассчитанного прогнозного значения 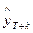 рассматриваемого процесса. В общем случае такая оценка может быть получена, основываясь на информации, характеризующей степень неопределенности как в инструментарии прогнозирования (модели), так и в исходных данных - прогнозном фоне. Эта неопределенность обычно выражается характеристиками соответствующих ошибок. Так, неопределенность модели определяется ошибками ее параметров, характеристики которых заданы в виде их ковариационной матрицы - Соv(а)).
рассматриваемого процесса. В общем случае такая оценка может быть получена, основываясь на информации, характеризующей степень неопределенности как в инструментарии прогнозирования (модели), так и в исходных данных - прогнозном фоне. Эта неопределенность обычно выражается характеристиками соответствующих ошибок. Так, неопределенность модели определяется ошибками ее параметров, характеристики которых заданы в виде их ковариационной матрицы - Соv(а)).
В отношении прогнозного фона на практике обычно рассматривают два возможных варианта его неопределенности. Согласно первому из них прогнозный фон рассматривается как набор детерминированных показателей, т.е. предполагается, что значения независимых переменных определены точно с нулевой ошибкой. Такая ситуация возможна при разработке некоторых безусловных прогнозов, например, на основе моделей с лаговыми зависимыми переменными. Однако в большинстве случаев прогнозный фон нельзя считать детерминированным. В самом деле, для моделей авторегрессии, в частности, детерминированный эндогенный прогнозный фон имеет место, только при разработке прогноза на момент Т+1. Значение 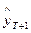 , используемое в расчете следующего прогнозного значения
, используемое в расчете следующего прогнозного значения 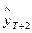 , уже определено. Аналогично нет никаких гарантий, что и при экзогенном прогнозном фоне значения факторов
, уже определено. Аналогично нет никаких гарантий, что и при экзогенном прогнозном фоне значения факторов 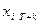 , i =1, 2,..., п, k = 1,2, …, относящиеся к будущим моментам времени, определены абсолютно точно. Обычно эти значения также получают в ходе каких-либо прогнозных исследований (например, с использованием методов экспертного прогнозирования). В таких случаях обычно оцениваются и соответствующие характеристики ошибки их прогнозов.
, i =1, 2,..., п, k = 1,2, …, относящиеся к будущим моментам времени, определены абсолютно точно. Обычно эти значения также получают в ходе каких-либо прогнозных исследований (например, с использованием методов экспертного прогнозирования). В таких случаях обычно оцениваются и соответствующие характеристики ошибки их прогнозов.
 2014-02-02
2014-02-02 2522
2522







