Глоссарий. Автокорреляция - корреляционная связь между значениями одного и того же случайного процесса х(t) в моменты времени t1 и t2

АВТОКОРРЕЛЯЦИЯ - корреляционная связь между значениями одного и того же случайного процесса х(t) в моменты времени t₁ и t₂. Функция, характеризующая эту связь, называется автокорреляционной. При анализе временных рядов автокорреляционная функция характеризует внутреннюю зависимость между временным рядом и тем же рядом, сдвинутым на некоторый промежуток (сдвиг) времени. Иначе говоря, это корреляция членов ряда и передвинутых на L единиц времени членов того же ряда: х₁, х₂, х₃ … и х_1+L, х_2+L, х_3+L… Запаздывание L называется лагом и является целым положительным числом.

акция - ценная бу­мага, удостоверяющая долевое участие в собственности (в ус­тавном фонде акционерного общества, эмитировавшего эту акцию). Обычно выпускаются ак­ции двух категорий: 1) про­стые или обыкновенные — дающие право голоса в управ­лении обществом, 2) привиле­гированные, такого права не дающие, но предоставляющие приоритет в получении диви­дендов. Курс отдельной акции должен быть достаточно вы­соким, чтобы норма дивиден­дов (годовые дивиденды, де­ленные на курс акций) плюс норма ожидаемого прироста капитала (общая прибыль ) ком­пенсировали вкладчику риск,связанный с владением акци­ей. Кривая спроса по обычным акциям почти бесконечно эла­стична (представляя собой го­ризонтальную прямую), но са­ма кривая может двигаться вверх и вниз в ответ на изме­нения ожидаемой прибыли, размеров риска и других пере­менных.

«БЕЛЫЙ ШУМ» - стационарный временной ряд, у которого математическое ожидание равно нулю, а ошибки ε_t некоррелированы. Возмущения (ошибки) ε_t в классической линейной регрессионной модели образуют «белый шум», а в случае их нормального распределения – нормальный (гауссовский) «белый шум».

ВАЛЮТНЫЕ ФЬЮЧЕРСЫ - соглашение, которое означает обязательство (а не право выбора в отличие от опциона) продать или купить стандартное количество конкретной валюты на определенную дату (в будущем) по курсу, установленному при заключении сделки. Разница между валютным курсом дня заключения и исполнения фьючерсной сделки называется спрэд. В стандартных контрактах регламентируются все условия: сумма, срок, гарантийный депозит, метод расчета. Тип контракта определяется суммой валюты и месяцем его исполнения.

Временные данные (временной ряд) – это совокупность экономической информации, характеризующей определенный объект за несколько последователь­ных моментов времени. Отдельный временной ряд можно считать выборкой из бесконечного ряда значений показателей во времени (например, данные о динамике фондовых индексов). Значение у(t) временного ряда формируется под влиянием сочетания длитель­ных, кратковременных и случайных факторов. Факто­ры, действующие в течение длительного времени, оказывают на изучаемое явление определяющее вли­яние и формируют основную тенденцию ряда — тренд Т(t). Периодические факторы формируют сезонные колебания ряда S(t). Случайные факторы отражаются случайными изменениями уровней ряда ε(t). Аддитивная модель, в которой временной ряд представлен как сумма перечисленных компонент, имеет вид: у(t) = Т(t) + S(t) + ε(t). Мультипликативная модель, в которой временной ряд представлен как произведение пере­численных компонент: у(t) = Т(t) · S(t) · ε(t). Выбор одной из двух моделей осуществляется на основе анализа сезонных колеба­ний. Основная задача эконометрического исследова­ния временного ряда — выявить каждую из перечис­ленных компонент ряда. Если амплитуда сезонных колебаний близка к по­стоянной, то используют аддитивную модель, если амплитуда существенно меняется — возрастает или убывает, то используют мультипликативную модель. Для моделирования временных рядов использу­ют модели парной линейной и нелинейной регрессии, множественной линейной и нелинейной регрессии и множество специальных моделей.

Гиперболическая функция (гипербола) - функция вида

,

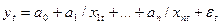где у_t - объясняемые (зависимые)результативные переменные, i = 1,2, …, n, случайные величины;

х_it - объясняющие (независимые), факторные переменные, неслучайные величины;

a₀, a_{1 …}a_n- неизвестные параметры модели регрессии;

ε_t - случайная ошибка регрессионной модели.

дисперсия — ха­рактеристика рассеивания зна­чений случайной величины, из­меряемая квадратом их от­клонений от среднего значе­ния (обозначается σ²). Разли­чается дисперсия теоретического (неп­рерывного или дискретного) и эмпирического (также непре­рывного и дискретного) рас­пределений. Для наиболее час­то применяемого в экономике эмпирического (дискретного) распределения дисперсия оп­ределяется по формуле: 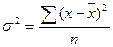, где х — наблюдаемая случай­ная величина, 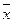— средняя исследуемого ряда, п — число элементов этого ряда. Есть и другие способы ее расчета, например: 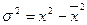. Квадратный корень из дисперсии называется средним квадратичным (квадратическим) отклонением или стандартным отклонением: отношение сред­него квадратического отклоне­ния к средней величине на­зывается коэффициентом ва­риации. В теории вероятностей вы­борочная дисперсия с увеличением числа наблюдений асимптоти­чески приближается к теоре­тической. Это свойство назы­вается состоятельностью оцен­ки дисперсии.

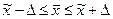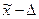доверительный интервал - предельные значения характеристик генеральной совокупности при заданной вероятности Р (доверительной), представляющей собой вероятность того, что ошибка выборки не превысит некоторую заданную величину, т.е. доверительный интервал для генеральной средней: (от до 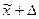), доверительный интервал для генеральной доли: 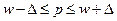(от w – Δ до w+Δ).

Закон нормального распределения характерен для распределения равновероятных событий, происходящих при взаимодействии множества случайных факторов. Такая закономерность проявляется в распределении отклонений, например, предоставляемых услуг связи от установленной нормы по качеству, предприятий по уровню эффективности использования ресурсов, работников по уровню выработки, заработной платы, квалификации, в распределении погрешностей измерений при проведении статистического наблюдения. Закон нормального распределения лежит в основе статистических методов оценки параметров распределения, репрезентативности выборочных наблюдений, измерения взаимосвязи массовых явлений. Нормальное распределение или закон Гаусса-Лапласа описывается уравнением

y_t = ,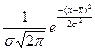

где y_t – ордината кривой нормального распределения, или частость (вероятность) величины х нормального распределения; 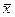– математическое ожидание (среднее значение) индивидуальных значений х.

Если значения (х – 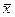) измерить (выразить) в величинах среднего квадратического отклонения σ, т.е. в стандартизованных (нормированных) отклонениях t = (x – 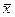)/σ, то формула примет вид

y_t = .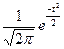

Нормальное распределение социально-экономических явлений в чистом виде встречается редко, однако, если соблюдена однородность совокупности, часто фактические распределения близки к нормальному. Закономерность распределения изучаемых величин выявляют посредством проверки соответствия эмпирического распределения теоретически нормальному закону распределения. Для этого фактическое распределение выравнивается по кривой нормального и рассчитываются критерии согласия. Нормальное распределение характеризуется двумя существенными параметрами, определяющими центр группирования индивидуальных значений и форму кривой: средней арифметической 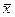и средним квадратическим отклонением σ. Кривые нормального распределения различаются положением на оси абсцисс центра распределения 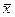и разбросом вариант около этого центра σ (рис. 3.7, 3.8). Особенностью кривой нормального распределения является ее симметричность относительно центра распределения – по обе стороны от ее середины образуются две равномерно убывающие ветви, асимптотически приближающиеся к оси абсцисс. Поэтому при нормальном распределении средняя, мода и медиана совпадают: 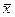= Мо = Ме.

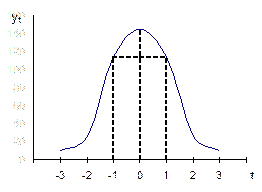
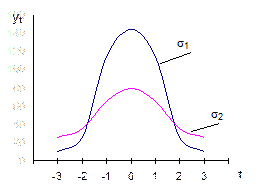
Рис. Г.1. Нормальное распределение

Рис. Г.2. Нормальное распределение с различными дисперсиями (σ12 < σ22)

Кривая нормального распределения имеет две точки перегиба (переход от выпуклости к вогнутости) при t = ±1, т.е. при отклонении вариантов от средней (х – 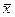), равном среднему квадратическому отклонению σ. В пределах 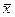± σ при нормальном распределении заключается 68,3%, в пределах 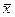±2σ – 95,4%, в пределах 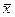±3σ – 99,7% количества наблюдений или частот ряда распределения. На практике почти не встречаются отклонения, превышающие ± 3σ, поэтому приведенное соотношение называется «правилом трех сигм».

классическая нормальная линейная модель множественной регрессии - модель множественной линейной регрессии, в которой зависимая переменная, возмущения и объясняющие переменные удовлетворяют условиям Гаусса-Маркова и, кроме того, предпосылке о невырожденности матрицы (независимости столбцов) значений объясняющей переменной.

классическая нормальная линейная регрессионная модель – модель парной линейной регрессии, для которой выполняются условия Гаусса-Маркова, случайный член ε_i имеет нормальное распределение, его значения некоррелированы и независимы.

ковариация (корреляционный момент) 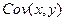случайных величин х и у – это математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е. 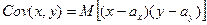, где а_х = М(х), а_у = М(у). Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и рассеяние вокруг точки (а_х, а_у). Ковариация – величина размерная, что затрудняет ее использование для оценки степени зависимости случайных величин (этих недостатков лишен коэффициент корреляции).

коэффициент детерминации (совокупный коэффициент множественной детерминации) R², равный квадрату совокупного коэффициента множественной корреляции; показывает, какая часть вариации результативного признака обусловлена влиянием факторов, включенных в модель. Является одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, характеристикой прогностической силы анализируемой эконометрической модели. Его величина показывает, какая часть (доля вариации) зависимой переменной обусловлена вариацией объясняющей переменной. 0 £ R² ³ 1, чем R² ближе к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии и между переменными х и у существует линейная функциональная зависимость. Если R² = 0, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.

коэффициент множественной корреляции (совокупный коэффициент множественной корреляции) R оценивает тесноту связи между результативным признаком и всеми факторами. Это основной показатель линейной множественной корреляции. Для двухфакторной модели совокупный коэффициент множественной корреляции рассчитывается по формуле

,

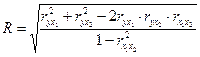где r_yx1, r_yx2, r_x1x2– парные коэффициенты корреляции между соответствующими признаками, которые измеряют тесноту линейной связи между факторами и между результативным признаком и каждым из рассматриваемых факторов без учета их взаимодействия с другими факторами.

Совокупный коэффициент корреляции R изменяется от 0 до 1. Чем меньше эмпирические значения результативного признака отличаются от выровненных по линии множественной регрессии, тем корреляционная связь между исследуемыми показателями теснее и совокупный коэффициент множественной корреляции ближе к единице.

коэффициенты эластичности (частные коэффициенты эластичности) используют для оценки сравнительной силы влияния факторов. Поскольку коэффициенты регрессии между собой несопоставимы (факторы имеют разные единицы измерения), то нельзя сравнивать силу влияния каждого из включенных в модель факторов на результативный признак на основании коэффициентов регрессии. Для оценки сравнительной силы влияния факторов рассчитывают частные коэффициенты эластичности и b-коэф­фициенты. Частные коэффициенты эластичности рассчитываются отдельно по каждому фактору: 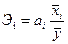, где а_i – коэффициент регрессии при i-м факторе; 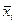– среднее значение i-го фактора; 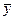– среднее значение результативного показателя.

Коэффициент эластичности показывает, на сколько процентов в среднем изменится результативный показатель при изменении фактора на 1% и фиксированном положении других факторов. Различия в степени варьирования вошедших в уравнение множественной регрессии факторов устраняются с помощью b–коэффициентов: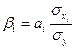, где s_xi, s_y – средние квадратические отклонения i-го фактора и результативного признака. Бета-коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак при изменении соответствующего фактора на величину его среднего квадратического отклонения.

КРИТЕРИЙ СТЬЮДЕНТА,t-критерий (t-статистика) Стьюдента, с помощью которого оценивают значимость коэффициентов уравнения регрессии. Вычисляется наблюдаемое зна­чение критерия t. Наблюдаемое значение t- критерия t_набл сравниваютсо значением t- критерия, определенным по таблице распределения Стьюдента (с критическим значением) t_табл. Критическое значением t-критерия t_табл (a; n-k) зависит от уровня значимости и числа степеней свободы. Уровень значимости a определяется как a = 1 - g, где величина g - доверительная вероятность попадания оцениваемого параметра в доверительный интервал. Доверительную вероятность необходимо брать близкую к единице (0,99; 0,95). Число степеней свободы определяется как разность между объемом выборки (n) и числом оцениваемых параметров по данной выборке (k). Для модели парной линейной регрессии число степеней свободы равно (n-2), т.к. по выборке оцениваются только 2 параметра (a₀ и a₁). Наблюдаемое значение t-критерия Стьюдента для проверки гипотезы о незначимости коэффициентов модели регрессии: 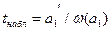, где a₁' - оценка коэффициента модели регрессии a₁, w (a₁) - величина стандартной ошибки коэффициента модели регрессии a₁.

Если модуль наблюдаемого значения t -критерия больше критического значения t -критерия | t _набл | > t _табл ,то с вероятностью (1 - a) основная гипотеза о незначимости коэффициентов модели регрессии отвергается (коэффициенты модели регрессии значимо отличаются от нуля). Если модуль наблюдаемого значения t -критерия меньше или равен критическому значению t -критерия | t _набл | £ t _табл ,то с вероятностью a основная гипотеза о незначимости коэффициентов модели регрессии принимается (коэффициенты модели регрессии почти не отличаются от нуля или равны нулю).

критерий Фишера-Снедекора, F-критерий (F-статистику) определяют для проверки значимости уравнения регрессии. Уравнение регрессии значимо на уровне a,если

,

где 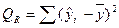,,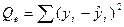 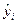- теоретическое значение зависимой переменной у;

n – 2 – число степеней свободы.

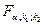– табличное значение F – критерия Фишера-Снедекора, определенное на уровне значимости a при k₁ = m - 1 и k₁ = n – m степеняхсвободы (при парной линейной регрессии m = 2).

Если F > 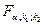, наблюдаемое значение F -критерия больше критического значения данногокритерия, определенного по таблице распределения Фишера-Снедекора, то с вероятностью a основная гипотеза о незначимости парного коэффициента детерминации или коэффициента модели регрессии отвергается, и модель парной регрессии значимо отличается от нуля.

Если F < 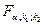, наблюдаемое значение F -критерия меньше критического значения данногокритерия, то с вероятностью (1-a) основная гипотеза о незначимости парного коэффициента детерминации или коэффициента модели регрессии принимается, и полученная модель парной регрессии является незначимой.

Линейная функция – функция вида ,

где у_t - объясняемые (зависимые)результативные переменные, случайные величины;

х_it - объясняющие (независимые), факторные переменные, неслучайные величины; i = 1,2, …, n;

a₀, a_{1 …}a_n- неизвестные параметры модели регрессии;

ε_t - случайная ошибка регрессионной модели.

ЛОЖНАЯ КОРРЕЛЯЦИЯ – отсутствие причинной связи между явлениями, хотя корреляционная связь между ними установлена. Часто встречается при анализе временных рядов, когда параллельно снижаются или повышаются показатели, на самом деле совершенно не зависящие друг от друга.

парабола второго порядка - полином второй степени – 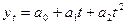, применяется в качестве аппроксимирующей функции при равномерном увеличении (уменьшении) цепных абсолютных приростов, т.е. монотонном изменении уровней ряда с возрастающей (убывающей) скоростью.

правая полулогарифмическая Функция - функция вида

,

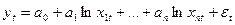где у_t - объясняемые (зависимые)результативные переменные,

ln х_it - натуральный логарифмобъясняющих (независимых) факторных переменных, неслучайные величины; i = 1,2, …, n, случайные величины;

a₀, a_{1 …}a_n- неизвестные параметры модели регрессии;

ε_t - случайная ошибка регрессионной модели.

лаговые (экзогенные или эндогенные) переменные относятся к предыдущим моментам времени и находятся в уравнении с переменными, относящимися к текущему моменту времени. Например, х_t-1 – лаговая экзогенная переменная, у_t-1 - лаговая эндогенная переменная.

логарифмическая гиперболическая функция - функция вида

,

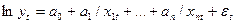где ln у_t - натуральные логарифмыобъясняемых (зависимых)результативных переменных, i = 1,2, …, n, случайные величины;

х_it - объясняющие (независимые), факторные переменные, неслучайные величины;

a₀, a_{1 …}a_n- неизвестные параметры модели регрессии;

ε_t - случайная ошибка регрессионной модели.

Метод наименьших квадратов (МНК), при котором рассчитывается сумма квадратов отклонений наблюдаемых значений результативной переменной у от теоретических значений у' (рассчитанных на основании функции регрессии f (x,a)). Согласно методу наименьших квадратов неизвестные параметры a₀ и a₁ выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений у_i от теоретических значений у'_i была минимальной:

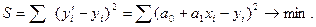
Метод наименьших модулей (МНМ), при котором рассчитываетсясумма модулей отклонений наблюдаемых значений результативной переменной у от теоретических значений у'. Согласно этому методу неизвестные параметры a₀ и a₁ выбираются таким образом, чтобы сумма модулей отклонений эмпирических значений у_i от теоретических значений у'_i была минимальной:

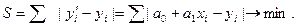
метод скользящей средней ( сглаживание с помощью скользящей средней, методподвижной средней) - метод преобразования рядов динамики, который состоит в последовательном вычислении средних величин по определенному числу членов ряда динамики, причем при вычислении каждой новой средней отбрасывается один член ряда слева и присоединяется один член ряда справа. Скользящая средняя может быть вычислена по трем, четырем, пяти и т.д. членам ряда динамики. Например, статистика связи использует метод средних для обнаружения тенденции изменения ряда динамики в силу свойств средней улавливать общие черты и свойства совокупности единиц, давать им обобщенную характеристику. Каждый раз, отбрасывая в числителе первый член и прибавляя последующий член ряда динамики, вычисляем средние величины, постепенно двигаясь вдоль ряда динамики. Скользящие средние достаточно четко показывают основную тенденцию изучаемого явления – наличие постоянного роста объема факсимильных сообщений. Для более плавного выравнивания ряда динамики следует брать для расчета средней большое количество членов ряда, например, пять. При этом нужно учитывать, что выровненный ряд оказывается короче первоначального ряда на два члена при расчете средней по трем членам, на четыре – при расчете средней по пяти членам и т.д. Слишком укороченный ряд скользящих средних может оказаться недостаточно убедительным для характеристики тенденции исследуемого ряда динамики.

модели авторегрессии – статистическое описание связи значений одного и того же показателя в разные моменты времени: 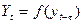. Объясняютвариацию результативной переменной в зависимости от предыдущих значений результативных переменных.

модели временных рядов представляют собой зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.

модели ожидания -объясняющие вариацию результативной переменной в зависимости от будущих значений факторных или результативных переменных.

модель парной (однофакторной) линейной регрессии представляет собой полином первой степени:

,

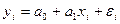где у_i - i-ое наблюдение зависимой переменной;

х_i - i-ые наблюдения объясняющих переменных, i = 1, 2, …, n;

ε_i - случайные ошибки регрессионной модели.

модели с распределенным лагом - объясняющие вариацию результативной переменной в зависимости от предыдущих значений факторных переменных.

Модель множественной линейной регрессии можно представить в следующем виде:

,

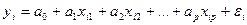где у_i - i-ое наблюдение зависимой переменной;

х_{i 1,} х_{i 2,} … х_{i p} - i-ые наблюдения объясняющих переменных, i = 1, 2, …, n;

ε_i - случайные ошибки регрессионной модели.

модель сезонности - зависимость результативной переменной от сезонной компоненты. Сезонность характеризует устойчивые внутригодовые колебания уровня показателя.

модель спроса и предложения состоит из трех уравнений: (двух поведенческих и одного тождества):

уравнение предложения ,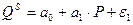

уравнение спроса ,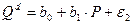

тождество равновесия ,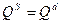

где Q^S - предлагаемое количество благ (объем предложения),

Q^d - спрашиваемое количество благ (объем спроса),

P - цена.

В этой системе 3 эндогенные переменные - Q^S, Q^d , P. При этом если переменные Q^S, Q^d представляют собой эндогенные переменные исходя из структуры самой системы (они расположены в левой части), то P является эндогенной переменнойпо экономическому содержанию (цена зависит от предлагаемого и спрашиваемого количества благ), а также в результатеналичия тождества Q^S = Q^d.

Модель тренда - зависимость результативной переменной от трендовой компоненты. Тренд представляет собой плавно изменяющуюся линию, отражающую устойчивое изменение уровня показателя в течение длительного периода времени и характеризующую тенденцию его динамики. Аналитическая формула этой линии устанавливается математическими методами, при этом выбор формы кривой должен быть обоснован экономически. Выравнивание может быть произведено по прямой или криволинейной зависимости, выражающей функциональную зависимость уровней ряда динамики от времени: 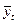= f(t). В основе нахождения аналитической функции выравнивания ряда динамики лежит теоретический анализ сущности данного явления и законов его развития.

модель тренда и сезонности - зависимость результативной переменной от трендовой и сезонной компоненты (см. также модель тренда, модель сезонности).

Мультиколлинеарность - это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. При наличии мультиколлинеарности оценки, полученные методом наименьших квадратов, формально существуют, но обладают ря­дом недостатков: 1) небольшое изменение исходных данных приводит к существенному изменению оце­нок регрессии; 2) оценки имеют большие стандарт­ные ошибки, малую значимость, при этом модель в целом является значимой (высокое значение коэф­фициента детерминации R²). Если при оценке уравнения регрессии несколько факторов оказались незначимыми, то нужно выяс­нить, нет ли среди них сильно коррелированных меж­ду собой. При наличии корреляции один из пары свя­занных между собой факторов исключается. Если статистически незначим лишь один фактор, то он должен быть исключен или заменен другим показате­лем. В модель регрессии включаются те факторы, которые более сильно связаны с зависимой перемен­ной, но слабо связаны с другими факторами.

облигация — цен­ная бумага, представляющая собой долговое обязательство правительства или фирмы и гарантирующая владельцу воз­врат долга в течение некоторого периода времени в форме регулярных выплат оп­ределенной суммы денег, вы­игрышей или другими спосо­бами. Применяются облига­ции, обеспеченные физиче­скими активами, доходом, об­лигации с возрастающей стои­мостью.

обратная линейная (функция Торнквиста) - функция вида

,

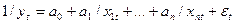где у_t - объясняемые (зависимые)результативные переменные,

ln х_it - натуральный логарифмобъясняющих (независимых) факторных переменных, неслучайные величины; i = 1,2, …, n, случайные величины;

a₀, a_{1 …}a_n- неизвестные параметры модели регрессии;

ε_t - случайная ошибка регрессионной модели.

Общий вид модели парной линейной регрессии зависимости переменной у от переменной х в генеральной совокупности:

,

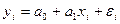где у_i - объясняемые (зависимые)результативные переменные, i = 1,2, …, n, случайные величины;

х_i - объясняющие (независимые), факторные переменные, неслучайные величины;

a₀, a₁ - неизвестные параметры модели парной регрессии;

ε_i - случайная ошибка регрессионной модели.

Опцион — согла­шение о том, что потенциальному покупателю или потенциальному продавцу предос­тавляется право приобрести или продать данный товар или ценную бумагу в опреде­ленный срок и по согласован­ной цене. Это означает, на­пример, что в случае повы­шения в процессе торговли цены на выбранный покупа­телем товар, покупатель мо­жет выиграть разницу в цене. На рынке ценных бумаг опционом называют право купить или продать ценные бумаги по ус­тановленному курсу, обуслов­ленное уплатой специальной премии. Различают опционы на продажу (пут-опцион) и на покупку(колл-опцион), а также двусторонние.

остаточная дисперсия - мера отклонения зависимой переменной от значений, предсказываемых уравнением регрессии, которая определяется следующим образом:

,

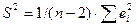где S² – остаточная дисперсия;

е_i – остаток, т.е. разница между измеренным и рассчитанным с помощью уравнения регрессии значениями зависимой переменной;

n – число пар переменных в выборке;

i – порядковый номер пары переменных в выборке.

предопределенные (объясняющие) переменные - к ним относятся лаговые (х_t-1) и текущие (х) экзогенные переменные, а также лаговые эндогенные переменные (у_t-1).

Пространственные данные – это совокупность экономической информации, характеризующей разные объекты и полученной за определенный период или момент времени. Пространственные данные являются выборочной совокупностью из некоторой генеральной совокупности (например, совокупность различной информации по предприятию – размер основных фондов, численность работников).

Регрессионный анализ – это процесс определения аналитического выражения функции связи, в котором изменение результативной или зависимой переменной происходит под влиянием факторной, или независимой переменной.

регрессионные модели с одним уравнением, в которых результативная (зависимая) переменная y может быть представлена в виде функции факторных (независимых) переменных x₁ … x_n:

,

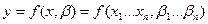где b₁ … b_n - параметры регрессионной модели.

СИСТЕМА ОДНОВРЕМЕННЫХ УРАВНЕНИЙ – система уравнений, в которой зависимая переменная одного уравнения может появляться одновременного в виде независимой переменной в одном или нескольких других уравнений. В этом случае теряет смысл традиционное различение зависимых и независимых переменных. В этом случае устанавливается различие между эндогенными и экзогенными переменными.

спецификации — один из этапов построения эконометрической модели, на котором на основании предварительного анализа рассматриваемого экономического объекта или процесса в математической форме выражаются обнаруженные связи и соотношения, а значит параметры и переменные, которые на данном этапе представляются существенными для цели исследования. В эконометрических моделях производится также спецификация ошибки, т.е. выбор некоторого типа распределения для случайного элемента модели, подлежащего оцениванию. Ошибкой спецификации называются: неправильный выбор типа связей и соотношений между элементами модели, а также выбор, в качестве существенных, таких переменных и параметров, которые на самом деле таковыми не являются, и наконец, отсутствие в модели некоторых существенных переменных.

Степенная функция - функция вида

,

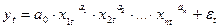где у_t - объясняемые (зависимые)результативные переменные, i = 1,2, …, n, случайные величины;

х_it - объясняющие (независимые), факторные переменные, неслучайные величины;

a₀, a_{1 …}a_n- неизвестные параметры модели регрессии;

ε_t - случайная ошибка регрессионной модели.

Теорема Гаусса-Маркова. Если условия Гаусса-Маркова выполняются, то оценки сделанные с помощью МНК, являются наилучшими оценками. Они обладают свойствами:

- несмещенности, это означает отсутствие систематической ошибки в положении линии регрессии;

- эффективности – имеют наименьшую дисперсию в классе всех линейных несмещенных оценок;

- состоятельности – при достаточно большом объеме данных оценки приближаются к истинным значениям.

условия Гаусса-Маркова:

1. Математическое ожидание случайного члена в любом наблюдении должно быть равно нулю – М(ε_i)= 0.

2. Дисперсия случайного члена должна быть постоянной для всех наблюдений – D (ε_i)= s², s - теоретическое значение стандартной ошибки модели.

3. Случайные члены должны быть статистически независимы (некоррелированы) между собой.

4. Объясняющая переменная х должна быть неслучайной.

фиктивные переменные принимают как правило, два значения: 1, если данный признак присутствует в наблюдении; 0 — при его отсутствии. Если включаемый в рассмотрение качественный признак име­ет не два, а несколько значений, то используют несколько фиктив­ных переменных, число которых должно быть на единицу меньше числа значений признака. При назначении фиктивных переменных исследуемая совокупность по числу значений качественного при­знака разбивается на группы. Одну из групп выбирают как эталон­ную и определяют фиктивные переменные для остальных. Если качественный признак имеет 2 значения, то это можно отразить, введя 1 фиктивную переменную. Например, строится модель, характеризующая показатели организаций двух подотраслей связи: электросвязи и почтовой связи. Вводится фиктивная переменная, которой присваивается значе­ние 0, если данные относятся к предприятиям электросвязи, и значение 1, если данные относятся к предприятиям почтовой связи. Если качественный признак имеет 3 значения, то это можно отразить, введя 2 фиктивных переменных. Например, строится модель, характеризующая показатели предприятий 3 регионов, Вводится 1 фиктивная переменная, которой присваивается значе­ние 0, если данные относятся к предприятиям первого региона, и значение 1, если данные относятся к предприятиям двух других регионов. Второй фиктивной переменной присваивается значение 0, если данные относятся ко второму региону, и 1, если данные относятся к первому и третьему регионам. Введение в регрессию фиктивных переменных существенно улучшает качество оценивания.

Финансовый рынок представляет собой сложную эконо­мическую систему, которая является: 1) сферой проявления экономических отношений при рас­пределении созданной стоимости и ее реализации путем обмена денег на финансовые активы. Под финансовыми активами понимаются денежные ресурсы и инвестицион­ные ценности. Инвестиционные ценности есть инструмен­ты образования финансовых ресурсов (ценные бумаги, ва­лютные ценности, золото и др.); 2)совокупностью инвесторов-покупателей и инвесторов-продавцов, взаимодействие которых приводит в конечном результате к возможности обмена между ними;инструментом согласования интересов продавцов и покупателей финансовых активов; 3) сферой проявления экономических отношений между продавцами и покупателями финансовых активов. На фи­нансовом рынке сталкиваются спрос в лице покупателя финансовых активов и предложение в лице продавца этих активов. Каждый из них имеет свои интересы, которые мо­гут совпадать или не совпадать. При совпадении интересов происходит акт купли-продажи финансовых активов. А это означает реализацию стоимости и потребительской стоимо­сти, заключенных в данных активах; 3)сферой проявления отношений между стоимостью и потребительской стоимостью тех товаров, которые обра­щаются на этом рынке. Товары, обращающиеся на финансовом рынке, - это финансовые активы. К ним относятся деньги (как рубли, так и валюта), депозиты, ценные бумаги разных видов, ссудный капитал, драгоценные металлы и драгоценные камни, объекты недвижимости.

Финансовый рынок - это категория экономическая, ко­торая выражает экономические отношения по поводу реа­лизации стоимости и потребительской стоимости, заклю­ченной в финансовых активах. Эти экономические отноше­ния определяются объективными экономическими закона­ми и финансовой политикой государства, формирующими в конечном итоге сущность финансового рынка, т.е. связи и отношения как в самом рынке, так и во взаимосвязи с другими экономическими категориями.

Конъюнктура финансового рынка - это соотношение спроса и предложения как по отдельным видам финансо­вых активов (акции какого-либо акционерного общества), так и по всей массе финансовых активов (акции, облигации и т.п.), сложившееся в данный момент под влиянием различ­ных факторов. Основными факторами являются политичес­кая и социально-экономическая обстановка в стране, дохо­ды потребителей (покупателей, вкладчиков), уровень цен (кур­сов, дивидендов, процентных ставок, премий, дисконта). Изучение конъюнктуры предполагает систематическое наблюдение за рынком, за отклонением спроса от предло­жения финансовых активов. В зависимости от состояния спроса и предложения различают благоприятную и небла­гоприятную ситуацию.

Основным показателем конъюнктуры финансового рын­ка является цена (курс, дивиденд, дисконт, процентная став­ка, премия). В ней находит отражение влияние всех конъюнктурных показателей. Изменение конъюнктуры проявля­ется в движении рыночной цены. Нормальное развитие финансового рынка требует уста­новления правильного соотношения между спросом и пред­ложением финансовых активов, их сбалансированности. Соотношение между спросом и предложением является основной пропорцией рынка. Спрос и предложение финансовых активов должны находиться в динамическом равновесии, которое обеспе­чивает беспрепятственную реализацию всех предлагаемых на рынке активов при одновременном полном удовлетво­рении спроса на них. Условия реализации финансовых активов включают в себя конкретную экономическую ситуацию, сложившуюся на финансовом рынке в данный момент, состояние и мате­риально-техническая оснащенность пунктов по купле-про­даже финансовых активов, различные юридические, эконо­мические и организационные формы регулирования тор­говли финансовыми активами. Следует иметь в виду, что финансовые активы по срав­нению с товарами народного потребления и услугамиоб­ладают большой ликвидностью. Их можно купить и сра­зу же продать. Это создает хорошие условия для игры на финансовом рынке. Поэтому один и тот же субъект на фи­нансовом рынке всегда может выступать одновременно в роли покупателя и в роли продавца финансовых активов. Финансовый рынок представляет собой систему отдель­ных самостоятельных рынков (звеньев), в каждом из кото­рых выделяются рынки конкретных видов финансовых ак­тивов (сектора). Финансовые рынки можно классифицировать по сфере распространения, по основной группе финансовых активов, по видам финансовых активов, по степени органи­зованности.

форвардный контракт - сделка с иностранной валютой, при которой стороны договариваются о поставке обусловленной суммы иностранной валюты через определенный срок после заключения сделки по курсу, зафиксированному в момент ее заключения.

функция с постоянной эластичностью замены – функция вида

,

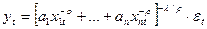где у_t - объясняемые (зависимые)результативные переменные, случайные величины;

х_it - объясняющие (независимые), факторные переменные, неслучайные величины; i = 1,2, …, n;

a₀, a_{1 …}a_n- неизвестные параметры модели регрессии;

l и r - также параметры функции;

ε_t - случайная ошибка регрессионной модели.

численность выборки - необходимый объема выборки, его расчет проводится с помощью преобразования формул предельных ошибок выборки Δ, соответствующих различным способам отбора.

Так, для случайного повторного отбора имеем 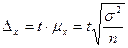, откуда 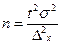. При случайном повторном отборе объем (необходимая численность) выборки прямо пропорционален квадрату коэффициента доверия t² и дисперсии вариационного признака σ ² и обратно пропорционален квадрату возможной ошибки выборки Δ². Для уменьшения предельной ошибки, например, в 2 раза численность выборки должна быть увеличена в 4 раза. Из трех параметров два (t и Δ) задаются исследователем, и трудность заключается в установлении размера выборочной дисперсии. Для этого используется вся информация, имеющаяся в распоряжении исследователя: данные подобных и пробных исследований, результаты предыдущих исследований.

При бесповторном отборе необходимая численность выборки рассчитывается по формуле 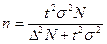. При прочих равных условиях при бесповторном отборе требуется меньший объем выборочной совокупности, чем при повторном.

При изучении альтернативного признака (доли р) необходимый объем выборки определяется по формулам при отборе: повторном 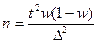, бесповторном .

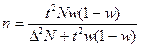экзогенные (независимые) переменные (х), значения которых задаются извне. В определенной степени данные переменные являются управляемыми.

Эконометрика – это наука, изучающая количественные закономерности и связи в экономике методами математической статистики.

экспоненциальная функция – функция вида

,

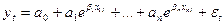где у_t - объясняемые (зависимые)результативные переменные, случайные величины;

х_it - объясняющие (независимые), факторные переменные, неслучайные величины; i = 1,2, …, n;

a₀, a_{1 …}a_n- неизвестные параметры модели регрессии;

b₁, …, b_n - также параметры функции;

ε_t - случайная ошибка регрессионной модели.

эндогенные переменные (у), значения которых определяются внутри модели.

эффект «эмерджентности» выражается в том, что со­вокупное воздействие нескольких факторов на переменную у, может значи­тельно отличаться от суммы воздействий каждого из них именно в силу наличия внутренних взаимосвязей между независимыми переменными.

[1] В рассматриваемой формулировке число параметров всех уравнений. В общем случае число параметров в каждом уравнении может различаться.