Алгоритм решения транспортной задачи на основе метода потенциалов

1. Находится первый опорный план по одному из рассмотренных методов.

2. Проверяется найденный опорный план на оптимальность, для чего:

2.1. Находятся потенциалы поставщиков 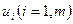и потребителей 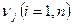по формуле .

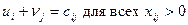Примечание. Так как в опорном плане заполнено т + п - 1 клеток таблицы транспортной задачи, то для нахождения потенциалов по данному плану можно составить систему из
т + п -1 линейно независимых уравнений с т + п неизвестными. Такая система является неопределенной, и поэтому одной неизвестной (обычно и_i придают нулевое значение, а остальные находятся однозначно по формуле .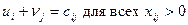

2.2. Проверяется, выполнено ли условие 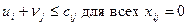или, что тоже самое, услови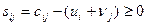е, , где 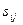— характеристика каждой свободной клетки таблицы. Если для всех свободных клеток таблицы условие 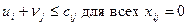выполнено, т.е. 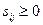, то опорный план транспортной задачи является оптимальным (решение задачи завершено). Если же для некоторых свободных клеток таблицы 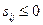, то клетка с наименьшим значением 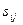является перспективной, и выполняется следующий пункт алгоритма.

2.3. К перспективной клетке строится цикл, расставляются знаки по циклу, при этом в перспективную клетку ставится плюс, а остальные знаки в вершинах цикла чередуются, и определяется величина перераспределения груза по формул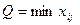е , где 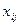— объем перевозки груза, записанный в клетках (вершинах) цикла таблицы, отмеченных знаком минус.

2.4. Осуществляется перераспределение груза по циклу на величину Q. В результате выполнения этого пункта будет получен новый опорный план, который проверяется на оптимальность, т.е. производится переход к пункту 2.1 алгоритма.

Дополнительные условия в транспортных задачах

В практике обычно при составлении экономико-математической модели задачи транспортного типа приходится вводить целый ряд дополнительных ограничений, вследствие чего поиск оптимального решения усложняется.

Рассмотрим наиболее часто встречающиеся случаи.

Нередко целесообразно минимизировать суммарные затраты на производство и транспортировку продукции. С подобной задачей можно столкнуться при решении вопросов, связанных с оптимальным размещением производственных объектов. Здесь может оказаться экономически более выгодным доставлять сырье из отдаленного источника, но зато при меньшей его себестоимости. В таких задачах критерием оптимальности служит сумма затрат на производство единицы груза и на его перевозку.

Часто необходимо вводить ограничения, согласно которым, отдельные поставки от определенного поставщика определенному потребителю должны быть исключены (из-за отсутствия достаточного количества транспорта или необходимых условий хранения груза, чрезмерной перегрузки коммуникаций и т. п.). Значит, в матрице перевозок, содержащей оптимальный план, определенные клетки должны остаться свободными. Это достигается искусственным завышением показателей 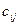в клетках, перевозки через которые следует запретить, до значений, заведомо больших всех, с которыми их придется сравнивать в процессе решения задачи.

Иногда приходится учитывать ограничения по пропускной способности некоторых маршрутов. Если, например, по маршруту i-j можно провезти не более d единиц груза, то j- й столбец матрицы перевозок разбивается на два: j’-й и j’’. В первом спрос принимается равным разности между действительным спросом b_j и ограничением d, во втором — равным ограничению d. Тарифы 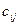в обоих столбцах одинаковы и равны данным, но в первом в клетке, соответствующей ограничению, вместо истинного тарифа 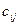ставится искусственно завышенный тариф М (клетка блокируется). Затем задача решается обычным способом.

Может случиться, что некоторые поставки по определенным маршрутам обязательны и должны войти в оптимальный план независимо от того, выгодно это или нет в условиях всей задачи. Тогда соответственно уменьшают запасы груза у поставщиков и спрос у потребителей и решают задачу относительно тех поставок, которые не обязательны.

Во многих задачах транспортного типа целевая функция максимизируется. Поэтому при составлении начального опорного плана в первую очередь стараются заполнять клетки, с наиболее высокими значениями показателя критерия оптимальности. Выбор клетки, подлежащей заполнению при переходе от одного опорного плана к другому, должен производиться не по отрицательной, а по положительной оценке. Оптимальным будет опорный план, которому в распределительной таблице сопутствуют свободные клетки с неположительными оценками.

Транспортная задача в сетевой постановке

Если условия транспортной задачи заданы в виде картосхемы, на которой условно изображены поставщики, потребители и связывающие их дороги, указаны величины запасов груза и потребностей в нем, а также числа 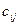являющиеся

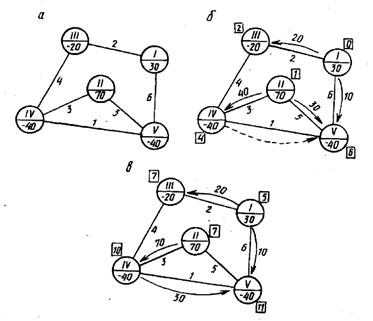
Рис.1

показателями принятого в задаче критерия оптимальности (тарифы, расстояния и т.п.), то говорят, что транспортная задача поставлена в сетевой форме (рис. 1, 2).

Описанную картосхему будем называть транспортной сетью. Пункты расположения поставщиков и потребителей будем изображать кружками и называть вершинами (узлами) сети, запасы груза будем записывать в кружках положительными, а потребности — отрицательными числами. Дороги, связывающие пункты расположения и потребления груза и другие пункты, будем изображать линиями и называть ребрами (дугами, звеньями) сети. При изображении транспортной сети реальный масштаб не соблюдается. На сети могут быть изображены вершины, в которых нет ни поставщиков, ни потребителей. Наличие таких вершин не повлияет на способ решения, если считать, что запасы (потребности) груза в них равны нулю.

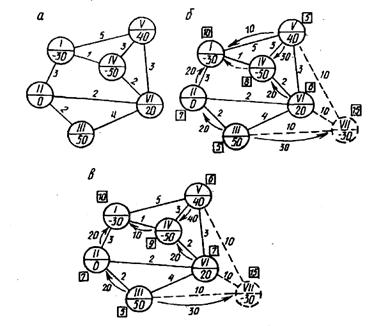
Рис.2

Такие вершины называют нулевыми (см. вершину II на рис. 2). Различия между транспортными задачами в матричной и сетевой формах весьма незначительны, так как методы их решения основаны на одних и тех же идеях. Далее мы будем использовать уже известный метод потенциалов.

Решение задачи на сети начинается с построения начального опорного плана. Поставки груза из вершины в вершину будем обозначать стрелками с указанием величин поставок.

Решение задачи на сети начинается с построения начального опорного плана.

Опорный план должен удовлетворять следующим требованиям:

1) все запасы должны быть распределены, а потребности удовлетворены;

2) к каждой вершине должна подходить или выходить из нее хотя бы одна стрелка;

3) общее количество стрелок должно быть на единицу меньше числа вершин;

4) стрелки не должны образовывать замкнутый контур

Далее следует проверить план на оптимальность.

Для этого вычисляют потенциалы. Одной из вершин (например, вершине I) присвоим некоторое значение потенциала (например, равное 0). (Для большей наглядности потенциалы заключают в рамки.) После этого, двигаясь по стрелкам, определяют потенциалы остальных вершин, руководствуясь правилом: если стрелка выходит из вершины, то к потенциалу этой вершины прибавляем показатель C_ij критерия оптимальности, если же направление стрелки противоположно, то C_ij вычитаем.

После вычисления потенциалов находят характеристики ребер без стрелок по правилу: из большего потенциала вычитается меньший, а разность вычитается из показателя C_ij, отвечающего данному ребру; если все ребра без стрелок имеют неотрицательные характеристики, то составленный план является оптимальным.

Если план неоптимален.

Для улучшения плана надо "загрузить" то ребро без стрелки, которому соответствует отрицательная характеристика. Если таких ребер несколько, то выбирается ребро с наибольшей по абсолютной величине отрицательной характеристикой и к нему подрисовывается новая стрелка. При этом образуется замкнутый контур из стрелок. Новая стрелка направляется от вершины с меньшим потенциалом к вершине с большим потенциалом.

При определении величины поставки для "загружаемого " ребра рассматриваются все стрелки образовавшегося контура (если на сети — опорный план, то такой контур всегда существует, причем только один!), имеющие направление, противоположное направлению новой стрелки, и среди них находится стрелка с наименьшей поставкой - А. Выбранная таким образом величина прибавляется ко всем поставкам со стрелками, имеющими то же направление, что и новая стрелка, и вычитается из поставок в стрелках, имеющих противоположное направление. Поставки в стрелках, не входящих в контур, сохраняются неизменными. Стрелка, по которой выбрано число А, ликвидируется, и общее число стрелок остается прежним.

Новый опорный план исследуется на оптимальность подобно предыдущему. Практически удобнее вести расчеты с положительными числами, поэтому значение первого (выбираемого произвольно) потенциала лучше брать равным не нулю, а какому-либо положительному числу.

Вырождение плана транспортной задачи в сетевой постановке внешне проявляется в том, что при полном использовании запасов и полном удовлетворении потребностей количество стрелок оказывается меньше, чем n - 1, где n - общее число вершин (включая и нулевые!).

Способ преодоления вырождения весьма прост: дополнительно вводится нужное количество стрелок с нулевыми поставками. Направления стрелок выбираются произвольно, однако они не должны образовывать замкнутый контур.

В случае открытой модели вводят фиктивного потребителя (поставщика) со спросом, равным небалансу. Фиктивный потребитель (поставщик) соединяется ребрами непосредственно со всеми поставщиками (потребителями). При этом показатели C_ij ребер, соединяющих фиктивного потребителя (поставщика) с поставщиками (потребителями), следует брать одинаковыми и сравнительно большими. Делается это для того, чтобы исключить возможность использования фиктивной вершины в качестве промежуточного пункта.