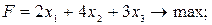

Отбрасывая требование целочисленности, решим заданную задачу как обычную задачу линейного программирования.
| БП | СЧ | 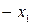 | 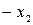 | 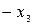 | CO |
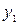 | 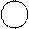 3 3 | 20/3 | |||
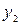 |  40/7 40/7 | ||||
| F | -2 | -4 | -3 |
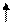
| БП | СЧ | 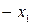 |  | 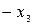 |
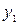 | 20/7 | -13/7 | -3/7 | -23/7 |
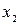 | 40/7 | 9/7 | 1/7 | 10/7 |
| F | 160/7 | 22/7 | 4/7 | 19/7 |
В полученном оптимальном решении задачи имеем нецелочисленное значение неизвестной х2. Дополнительное ограничение формируем по элементам второй строки:
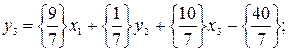
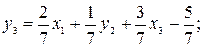
| БП | СЧ | 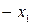 |  | 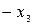 | CO |
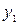 | 20/7 | -13/7 | -3/7 | -23/7 | - |
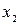 | 40/7 | 9/7 |  1/7 1/7 | 10/7 | |
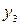 | -5/7 | -2/7 | -1/7 | -3/7 |  5 5 |
| F | 160/7 | 22/7 | 4/7 | 19/7 |
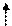
| БП | СЧ | 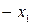 | 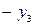 | 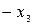 |
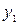 | ||||
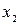 | ||||
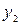 | ||||
| F |
Ответ: 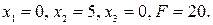
Метод ветвей и границ
Сначала в области допустимых решений системы ограничений находится оптимальное решение, в частности симплекс-методом без учета целочисленности. Если в полученном решении некоторые переменные имеют дробные значения, то выбираем любую из дробных переменных и по ней строим два ограничения. В одном ограничении величина этой переменной меньше либо равна наибольшему целому числу, не превышающему значения дробной переменной в оптимальном решении. В другом ограничении переменная больше или равна наименьшему целому значению, но не меньше значения дробной переменной.
Если, например, дополнительные ограничения строить по переменной 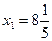 , то первое ограничение будет
, то первое ограничение будет 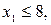 а второе
а второе 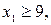 этим мы исключаем из ОДР исходной задачи промежуток с дробными значениями неизвестной
этим мы исключаем из ОДР исходной задачи промежуток с дробными значениями неизвестной  . Этот промежуток разбивает ОДР на две части
. Этот промежуток разбивает ОДР на две части
 ОДР
ОДР
ОДЗ1 ОДЗ2
В результате разбиения ОДР получены две новые задачи (подзадачи) линейной оптимизации. Если после их решения полученные значения неизвестных будут не целочисленные, то, сравнив значения функций этих задач, выбираем задачу с большим значением функции и по новой неизвестной с дробным значением строим снова два дополнительных ограничения (третье и четвертое) и разбиваем эту задачу еще на две новые подзадачи. В результате получаем ветви. Ветвление заканчивается нахождением целочисленного решения, если оно существует. Границами в методе выступают значения функций задач каждой ветви. На каждом этапе решения задачи дальнейшему ветвлению (разбиению на новые задачи) подлежит та ветвь (задача), у которой значение функции больше. Поэтому отдельные подзадачи (ветви), у которых, значение функции меньше, могут быть отброшены. Однако иногда, сравнивая значения функций подзадач, приходится возвращаться к ветвям, которые, ранее были отброшены, и продолжать дальнейшее решение от них.
Поскольку множество всех решений задачи ЦЛО конечно, то после конечного числа разбиений исходной задачи на подзадачи оптимальное решение будет найдено.
Проиллюстрируем применение метода ветвей и границ на следующем примере.
Пример. Найти максимум функции
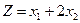
при ограничениях
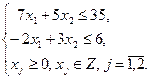
Решение. Для наглядности решение осуществим графическим методом. ОДР задачи является многоугольник ОАВС (рис. 1). В точке В находится максимальное значение функции: 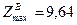 при
при 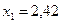 и
и 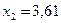

Рис. 1
Поскольку значения неизвестных дробные, то разобьём по неизвестной 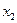 ОДР задачи на две части. Одна будет содержать множество точек, у которых
ОДР задачи на две части. Одна будет содержать множество точек, у которых 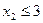 , а вторая — у которых
, а вторая — у которых 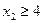 . В результате получаем две новые задачи линейной оптимизации: №2 и № 3 (исходная задача имеет № 1).
. В результате получаем две новые задачи линейной оптимизации: №2 и № 3 (исходная задача имеет № 1).
| Задача № 2 | Задача № 3 |
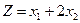 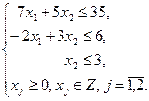 | 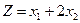 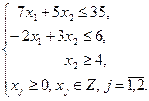 |
Области допустимых решений задач представлены на рис. 2.
Из рис. 2 видно, что ни одна целочисленная точка исходной ОДР не потеряна. ОДР задачи № 2 является многоугольник OADEC. В точке Е с координатами 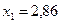 и
и 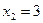 функция достигает максимального значения
функция достигает максимального значения 
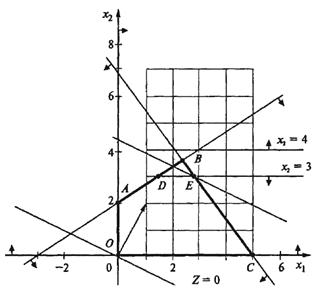
Рис. 2
Решение задачи № 2 не является целочисленным. Что касается задачи № 3, то ее ОДР пустая. Ограничения этой задачи противоречивы, и она не имеет решения.
Продолжая решение, разобьем ОДР задачи № 2 на два подмножества по неизвестной 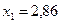 . В результате получим две новые задачи № 4 и № 5 с соответствующими дополнительными ограничениями:
. В результате получим две новые задачи № 4 и № 5 с соответствующими дополнительными ограничениями: 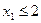 и
и 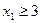 .
.
| Задача № 4 | Задача № 5 |
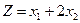  | 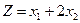 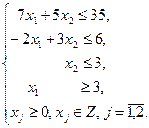 |
ОДР этих задач представлены на рис. 3.
ОДР задачи № 4 является многоугольник OADFK. Максимальное значение функции достигается в точке F с координатами 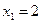 и
и 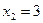 .
. 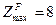 . Таким образом, получено целочисленное решение задачи № 4.
. Таким образом, получено целочисленное решение задачи № 4.
ОДР задачи № 5 является треугольник LMC. Максимальное значение функция достигает в точке L с координатами 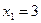 ;
; 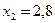 ;
; 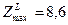
Так как значение функции целочисленного решения задачи № 4 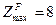 меньше
меньше 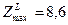 , то дальнейшему разбиению на две задачи № 6 и № 7 подлежит задача № 5 по нецелочисленной неизвестной
, то дальнейшему разбиению на две задачи № 6 и № 7 подлежит задача № 5 по нецелочисленной неизвестной 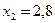 . Не проводя дополнительных построений, отметим, что ОДР задачи № 6 с дополнительным ограничением
. Не проводя дополнительных построений, отметим, что ОДР задачи № 6 с дополнительным ограничением 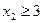 не существует, а значение функции в оптимальном целочисленном решении задачи № 7 с дополнительным ограничением
не существует, а значение функции в оптимальном целочисленном решении задачи № 7 с дополнительным ограничением  равно 7, что меньше
равно 7, что меньше 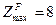 . Таким образом, целочисленное решение исходной задачи следующее:
. Таким образом, целочисленное решение исходной задачи следующее: 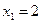 ,
, 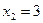 ,
, 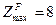 .
.
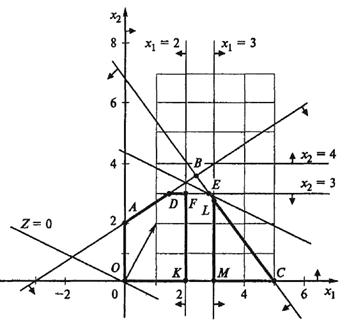
Рис. 3
 2014-02-02
2014-02-02 1600
1600








