Решение матричной игры сведением к задаче линейного программирования
Пусть игра задана платежной матрицей.
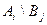 | 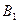 | 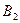 | … | 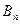 |
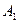 | 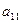 | 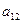 | … | 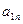 |
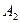 | 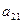 | 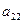 | … | 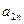 |
| … | … | … | … | |
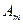 | 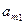 | 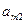 | … | 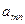 |
Оптимальные смешанные стратегии 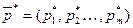 и
и 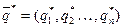 игроков А и В могут быть найдены в результате решения пары двойственных задач линейного программирования.
игроков А и В могут быть найдены в результате решения пары двойственных задач линейного программирования.
Для игрока А:
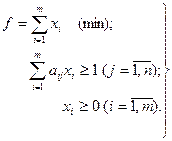
В результате решения задачи находятся оптимальный вектор 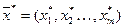 и
и 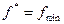 , а затем
, а затем 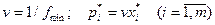 .
.
Для игрока В:
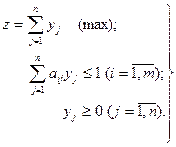
Решая задачу, находят оптимальный вектор 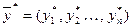 и
и 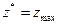 , а затем
, а затем 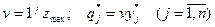 .
.
Решение матричной игры графическим методом
При поиске оптимальных стратегий в матричных играх размерностей 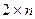 и
и 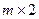 целесообразно использовать графический метод решения задач линейного программирования и свойства оптимальных планов пары двойственных задач: если в оптимальном плане задачи переменная положительна, то соответствующее ограничение двойственной задачи ее оптимальным планом обращается в равенство; если оптимальным планом задачи ограничение обращается в строгое неравенство, то в оптимальном плане двойственной задачи соответствующая переменная равна нулю.
целесообразно использовать графический метод решения задач линейного программирования и свойства оптимальных планов пары двойственных задач: если в оптимальном плане задачи переменная положительна, то соответствующее ограничение двойственной задачи ее оптимальным планом обращается в равенство; если оптимальным планом задачи ограничение обращается в строгое неравенство, то в оптимальном плане двойственной задачи соответствующая переменная равна нулю.
Пример. Решить игру с платежной матрицей
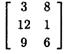 графическим методом.
графическим методом.
Решение. В данном случае 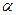 = 6,
= 6, 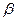 = 8, т.е.
= 8, т.е. 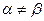 , а поэтому для определения оптимальных смешанных стратегий игроков составляем задачи
, а поэтому для определения оптимальных смешанных стратегий игроков составляем задачи
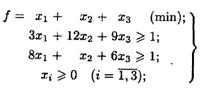
(1)
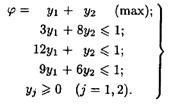
(2)
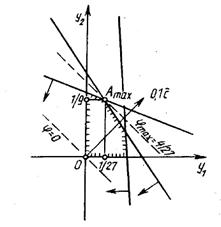
Поскольку одна из задач содержит две переменные, то, решим ее графически, находим: 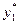 =1/27,
=1/27, 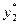 =1/9,
=1/9, 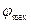 =4/27. Используя формулы
=4/27. Используя формулы 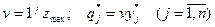 , получаем:
, получаем: 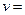 27/4,
27/4, 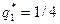 ,
,  .
.
Для определения оптимальной смешанной стратегии 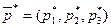 найдем сначала решение двойственной задачи. В оптимальном плане задачи (2)
найдем сначала решение двойственной задачи. В оптимальном плане задачи (2) 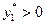 и
и 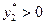 , поэтому оба ограничения двойственной задачи (1) ее оптимальным планом
, поэтому оба ограничения двойственной задачи (1) ее оптимальным планом 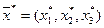 обращаются в равенства. Кроме того, значениями
обращаются в равенства. Кроме того, значениями 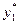 и
и 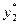 второе ограничение задачи (2) обращается в строгое неравенство. Следовательно, в оптимальном плане задачи (1) соответствующая ему вторая переменная равна нулю, т. е.
второе ограничение задачи (2) обращается в строгое неравенство. Следовательно, в оптимальном плане задачи (1) соответствующая ему вторая переменная равна нулю, т. е. 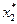 =0. Учитывая сказанное, для определения
=0. Учитывая сказанное, для определения 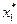 и
и 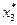 получаем уравнения
получаем уравнения 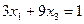 и
и 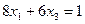 , совместное решение которых дает
, совместное решение которых дает 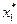 = 3/54,
= 3/54, 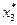 = 5/54. Используя формулы
= 5/54. Используя формулы 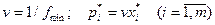 , определяем
, определяем 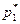 =3/8,
=3/8, 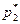 =0,
=0, 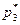 =5/8. Итак, решение игры найдено:
=5/8. Итак, решение игры найдено:
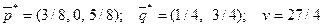 .
.
Решение игр с природой по различным критериям
Будем предполагать, что в игре с природой сознательный игрок А может использовать 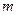 чистых стратегий
чистых стратегий 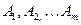 , а природа П может реализовывать
, а природа П может реализовывать 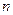 различных состояний
различных состояний 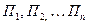 . Игроку А могут быть известны вероятности
. Игроку А могут быть известны вероятности 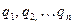 , с которыми природа реализует свои состояния, но он может и не знать их. Действуя против природы, игрок А имеет возможность использовать как чистые стратегии
, с которыми природа реализует свои состояния, но он может и не знать их. Действуя против природы, игрок А имеет возможность использовать как чистые стратегии 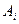 так и смешанные стратегии
так и смешанные стратегии 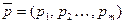 . Если игрок А в состоянии оценить (величиной
. Если игрок А в состоянии оценить (величиной  ) последствия применения каждой своей чистой стратегии
) последствия применения каждой своей чистой стратегии 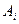 при любом состоянии
при любом состоянии 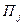 природы, то игру можно задать матрицей.
природы, то игру можно задать матрицей.
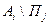 | 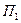 | 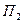 | … | 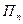 |
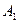 | 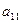 | 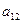 | … | 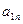 |
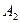 | 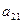 | 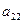 | … | 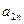 |
| … | … | … | … | |
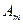 | 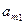 | 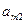 | … | 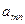 |
Поскольку игры с природой являются частным видом парных матричных игр, то вся теория стратегических игр переносится и на игры с природой. Однако игры с природой обладают и некоторыми особенностями. Например, при упрощении платежной матрицы отбрасывать те или иные состояния природы нельзя, так как она может реализовать любое состояние независимо от того, выгодно оно игроку А или нет. Другая особенность состоит в том, что решение достаточно найти только для игрока А, поскольку природа наши рекомендации воспринять не может. И ещё одна важная особенность: в играх с природой смешанные стратегии имеют ограниченное (главнымобразом теоретическое) значение: не всегда можно для них найти форму, удобную для использования в реальной обстановке. Смешанные стратегии приобретают смысл только при многократном повторении игры. В свете последнего замечания более естественными в играх с природой являются рекомендации в чистых стратегиях игрока А.
С учетом отмеченных особенностей сформулирован ряд критериев, которыми пользуются при выборе оптимальных стратегий игрока А в ситуациях, моделирующихся в игры с природой. Эти критерии основываются на здравом смысле, интуиции и практической целесообразности. Они дают некоторую логическую схему принятия решения. Критерии позволяют последовательным численным анализом ситуации с разных точек зрения оценить принимаемое решение и высказать рекомендации по тому или иному образу действий и тем самым выбрать что-то определенное. Если рекомендации, вытекающие из различных критериев, совпадают, принимается рекомендуемое решение. Если же рекомендации критериев противоречат друг другу, то необходимо сравнить, насколько значительно отличаются результаты по разным критериям, привлечь дополнительную информацию и сделать окончательный выбор.
При выборе оптимальной стратегии игрока А опираются как на платежную матрицу, так и на матрицу рисков. Риском 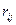 игрока А, когда он пользуется чистой стратегией
игрока А, когда он пользуется чистой стратегией 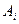 при состоянии
при состоянии 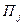 природы, называется разность между максимальным выигрышем, который он мог бы получить, если бы достоверно знал, что природой будет реализовано именно состояние
природы, называется разность между максимальным выигрышем, который он мог бы получить, если бы достоверно знал, что природой будет реализовано именно состояние 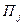 , и тем выигрышем, который он получит, используя стратегию
, и тем выигрышем, который он получит, используя стратегию 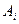 в неведении о том, какое же состояние
в неведении о том, какое же состояние 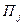 природа реализует. Таким образом, элементы
природа реализует. Таким образом, элементы 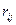 матрицы рисков определяются по формуле
матрицы рисков определяются по формуле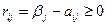 , где
, где 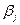 —максимально возможный выигрыш игрока А при состоянии
—максимально возможный выигрыш игрока А при состоянии 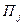 (максимальный элемент j- гостолбца платежной матрицы, т.е.
(максимальный элемент j- гостолбца платежной матрицы, т.е. 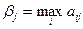 ). Итак, исследуя платежную матрицу, мы стремимся выбрать такое решение, чтобы выигрыш игрока А максимизировался, а анализируя матрицу рисков, стараемся минимизировать неизбежный риск, сопровождающий выбор решения.
). Итак, исследуя платежную матрицу, мы стремимся выбрать такое решение, чтобы выигрыш игрока А максимизировался, а анализируя матрицу рисков, стараемся минимизировать неизбежный риск, сопровождающий выбор решения.
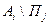 | 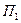 | 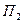 | … | 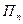 | 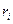 |
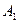 | 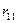 | 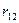 | … | 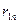 | 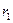 |
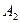 | 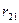 | 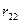 | … | 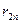 | 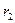 |
| … | … | … | … | … | |
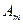 | 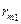 | 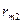 | … | 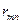 | 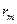 |
Если вероятности 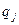 состояний
состояний 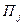 природы известны, то пользуются критерием Байеса, в соответствии с которым оптимальной считается чистая стратегия
природы известны, то пользуются критерием Байеса, в соответствии с которым оптимальной считается чистая стратегия 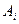 , при которой максимизируется средний выигрыш
, при которой максимизируется средний выигрыш 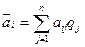 игрока А, т. е. обеспечивается
игрока А, т. е. обеспечивается
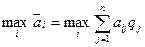 .
.
Если игроку А представляются в равной мере правдоподобными все состояния 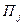 природы, то иногда полагают
природы, то иногда полагают 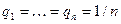 и, учитывая "принцип недостаточного основания" Лапласа, оптимальной считают чистую стратегию
и, учитывая "принцип недостаточного основания" Лапласа, оптимальной считают чистую стратегию 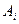 , обеспечивающую
, обеспечивающую
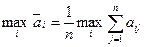 .
.
Если вероятности 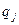 состояний совсем неизвестны и нельзя сделать о них никаких предположений, то пользуются критериями Вальда, Сэвиджа и Гурвица. Оптимальной по критерию Вальда считается чистая стратегия
состояний совсем неизвестны и нельзя сделать о них никаких предположений, то пользуются критериями Вальда, Сэвиджа и Гурвица. Оптимальной по критерию Вальда считается чистая стратегия 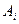 ,при которой наименьший выигрыш игрока А будет максимальным, т.е. ему обеспечивается
,при которой наименьший выигрыш игрока А будет максимальным, т.е. ему обеспечивается 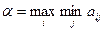 . В соответствии с этим критерием игра ведется как с разумным партнером, противодействующим игроку А в достижении успеха. Критерий рекомендует игроку А ожидать наихудшего результата и в этом предположении искать наиболее благоприятный исход (выигрыш), который совпадает с нижней чистой ценой игры. Критерий Вальда выражает позицию крайнего пессимизма, и принимаемое решение носит заведомо перестраховочный характер. Однако этот критерий имеет право на применение в практике вместе с другими критериями, оценивающими исследуемую ситуацию с других точек зрения.
. В соответствии с этим критерием игра ведется как с разумным партнером, противодействующим игроку А в достижении успеха. Критерий рекомендует игроку А ожидать наихудшего результата и в этом предположении искать наиболее благоприятный исход (выигрыш), который совпадает с нижней чистой ценой игры. Критерий Вальда выражает позицию крайнего пессимизма, и принимаемое решение носит заведомо перестраховочный характер. Однако этот критерий имеет право на применение в практике вместе с другими критериями, оценивающими исследуемую ситуацию с других точек зрения.
Оптимальной по критерию Сэвиджа считается та чистая стратегия 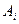 , при которой минимизируется величина
, при которой минимизируется величина 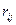 максимального риска, т. е. обеспечивается
максимального риска, т. е. обеспечивается 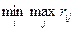 . Таким образом, критерий Сэвиджа советует ориентироваться не на выигрыш, а на риск. Это тоже критерий крайнего пессимизма, но здесь пессимизм понимается в ином свете: рекомендуется всячески избегать большого риска при принятии решения.
. Таким образом, критерий Сэвиджа советует ориентироваться не на выигрыш, а на риск. Это тоже критерий крайнего пессимизма, но здесь пессимизм понимается в ином свете: рекомендуется всячески избегать большого риска при принятии решения.
Оптимальной по критерию Гурвица считается чистая стратегия 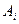 ,найденная из условия
,найденная из условия
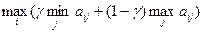 ,
,
где 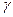 принадлежит интервалу (0; 1) и выбирается из субъективных соображений. При
принадлежит интервалу (0; 1) и выбирается из субъективных соображений. При 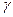 =1 критерий Гурвица превращается в критерий Вальда, при
=1 критерий Гурвица превращается в критерий Вальда, при 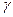 = 0 — в критерий крайнего оптимизма, когда рекомендуется выбирать стратегию, обеспечивающую самый большой выигрыш. В связи с этим критерий Гурвица называют критерием пессимизма-оптимизма. При
= 0 — в критерий крайнего оптимизма, когда рекомендуется выбирать стратегию, обеспечивающую самый большой выигрыш. В связи с этим критерий Гурвица называют критерием пессимизма-оптимизма. При
0 < 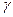 < 1 получается нечто среднее между тем и другим. Чем ответственнее ситуация, чем больше стремление подстраховаться в ней и не рисковать без должных оснований, тем ближе к единице выбирается коэффициент пессимизма
< 1 получается нечто среднее между тем и другим. Чем ответственнее ситуация, чем больше стремление подстраховаться в ней и не рисковать без должных оснований, тем ближе к единице выбирается коэффициент пессимизма 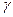 .
.
 2014-02-02
2014-02-02 3905
3905
