Матричные игры

Основные понятия

При решении ряда практических задач исследования операций, приходится анализировать ситуации, когда наряду, с неопределенностью сопровождающей какую-то операцию приходится сталкиваться с сознательным противодействием и результат зависит от того, какой образ действий выберет противник. Такие ситуации будем называть конфликтными.

Теория игр – это математическая теория конфликтных ситуаций. Её задача – выработка рекомендаций по рациональному образу действий участников конфликта.

Игрой будем называть упрощенную модель конфликтной ситуации. От реальной конфликтной ситуации она отличается тем, что ведется по определенным правилам.

Стороны участвующие в конфликтной ситуации называются «игроками». В зависимости от количества игроков различают парные и множественные игры. Мы будем рассматривать парные игры, т.к. они имеют наибольшее практическое значение.

Исход игры – это значение некоторой функции, называемой функцией выигрыша (платежной функцией). Эта функция задается либо таблицей, либо аналитическим выражением.

Игра называется игрой с нулевой суммой, если один игрок выигрывает ровно столько, сколько проигрывает другой, т.е. сумма выигрышей сторон равна нулю. Мы будем рассматривать только такие игры.

Ходом в теории игр называется выбор одного из предусмотренных правилами игры действий и его осуществление. Ходы бывают личные и случайные.

Личным ходом называется сознательный выбор игроком одного из возможных вариантов действий и его осуществление. Ход называется случайным, если выбор производится не игроком. А каким- либо механизмом случайного выбора (бросание монеты, выбор карты из колоды). Теория игр занимается анализом только тех игр, которые содержат личные ходы.

Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом ходе этого игрока в зависимости от ситуации, сложившейся в процессе игры.

Оптимальной стратегией игрока называется такая стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш (или минимально возможный средний проигрыш).

Игры, в которых оба участника сознательно стремятся добиться наилучшего для себя результата, называются стратегическими.

В экономической практике часто приходится моделировать ситуации, придавая им игровую схему, в которых один из участников безразличен к результату игры.

Такие игры называются «играми с природой», понимая под термином «природа» всю совокупность внешних обстоятельств, в которых сознательному игроку приходится принимать решение.

В играх с природой степень неопределенности при принятии решения сознательным игроком возрастает, т.к. «природа» будучи безразличной, к исходу игры может реализовывать такие состояния, которые ей совершенно невыгодны.

Платежная матрица

Рассмотрим игру, в которой игрок 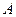имеет 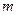стратегий, а игрок 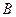(«противник») - 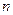стратегий. Такая игра называется игрой 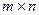. Наши стратегии будем обозначать 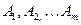, противника - 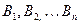. Предположим, что каждая сторона выбрала определенную стратегию: мы выбрали 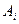, противник 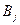. Выбор стратегии однозначно определяет исход игры – наш выигрыш, обозначим его .

Предположим, что нам известны значения для каждой пары стратегий. Эти значения можно записать в виде прямоугольной таблицы. Такая таблица называется платежной матрицей.

			…
			…
			…
	…	…	…	…
			…

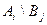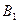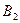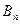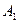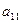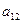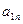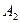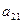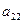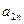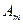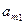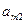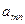Нижняя и верхняя цена игры

			…
			…
			…
	…	…	…	…	…
			…
			…

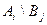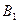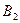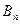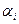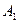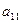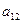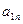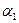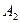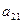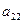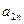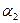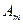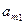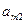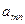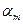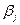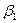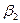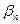В таблице приведены числа 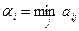- минимально возможный выигрыш игрока А, применяющего стратегию 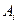(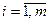) и 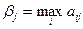- максимально возможный проигрыш игрока В, если он пользуется стратегией ().

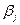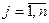Число 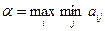называют нижней чистой ценой игры (максимином), а соответствующую ему чистую стратегию – максиминной.

Число 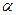показывает, какой минимальный гарантированный выигрыш может получить игрок А, правильно применяя свои чистые стратегии при любых действиях игрока В.

Число 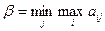называют верхней чистой ценой игры (минимаксом), а соответствующую чистую стратегию минимаксной.

Число 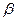показывает, какой минимальный гарантированный проигрыш может быть у игрока В, при правильном выборе им своих чистых стратегии независимо от действий игрока А.

Ясно, что .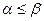

Если 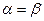, то говорят, что игра имеет седловую точку в чистых стратегиях и чистую цену игры 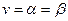. Стратегии образующие седловую точку, являются оптимальными. Тройку () называют решением игры.

Смешанные стратегии

Для игр без седловых точек оптимальные стратегии игроков находятся в области смешанных стратегий.

Смешанной стратегией игрока А называют вектор 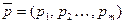, компоненты которого удовлетворяют условиям .

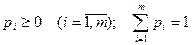Смешанной стратегией игрока В называют вектор 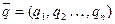, компоненты которого удовлетворяют условиям .

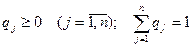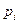и 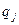- вероятности, с которыми игроки А и В выбирают свои чистые стратеги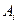и и 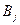в ходе игры.

При использовании смешанных стратегий игра приобретает случайный характер, случайной становится и величина выигрыша игрока А (проигрыша игрока В). Эта величина является функцией смешанных стратегий и 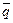и определяется по формуле .

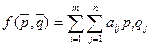Функцию называют функцией выигрыша или платежной функцией.

Смешанные стратегии называются оптимальными, если они образуют седловую точку для платежной функции , т.е. если они удовлетворяют неравенству .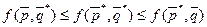

Величину 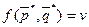называют ценой игры.

Поиск оптимальных смешанных стратегий начинают с упрощения платежной матрицы. Если в платежной матрице элементы k -й строки не меньше соответствующих элементов s -й строки, т. е. 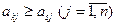, то говорят, что стратегия 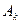доминирует над стратегией 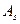. Аналогично, если элементы l -го столбца не превосходят соответствующих элементов r -го столбца, т. е. 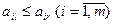, то говорят, что стратегия 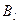доминирует над стратегией 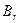. Частным случаем доминирования стратегий является дублирование стратегий, когда 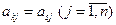или 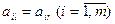. Исключение из платежной матрицы доминируемых стратегий (ими игрокам пользоваться заведомо невыгодно) позволяет уменьшить ее размерность, а это упрощает решение игры. Вероятность применения доминируемых стратегий равна нулю.

Оптимальные смешанные стратеги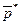и и 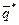в игре с платежной матрицей 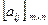и ценой v остаются оптимальными и для игры с платежной матрицей (где b > 0) и ценой bv + с. На этом основании платежную матрицу можно всегда преобразовать так, что ее элементы будут целыми неотрицательными числами, а это упрощает расчеты.