Математическая постановка задачи определения температурного поля в каком-либо теле требует описания баланса тепла каждой точки этого тела. Это описание обычно задаётся в дифференциальной форме и приводит к тому или иному уравнению теплопроводности.
Выведем это уравнение при следующих допущениях:
1) твердое тело однородно и изотропно, т.е. теплофизические характеристики материала не зависят от координат, температуры и времени;
2) внутри тела источники и стоки тепла отсутствуют;
3) в процессе теплопередачи не происходят фазовые превращения;
4) деформации, вызванные изменением температуры, пренебрежимо малы по сравнению с размерами тела;
5) температуры на элементарных площадках будем считать равномерно распределёнными.
Рассмотрим изменение теплосодержания элементарного объёма 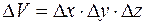 (рис.1.1).
(рис.1.1).
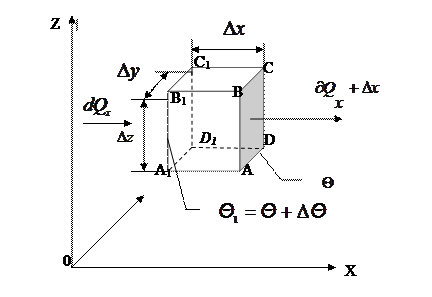
Рис. 1.1 Схема к выводу дифференциального уравнения теплопроводности
Пусть на грани ABCD температура распределена равномерно и имеет некоторое значение 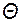 . На противоположной грани A1 B1 C1 D1 температура будет иметь значение
. На противоположной грани A1 B1 C1 D1 температура будет иметь значение 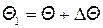 . Будем считать, что в направлении осей y и z тепло не распространяется
. Будем считать, что в направлении осей y и z тепло не распространяется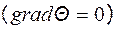 .
.
За время 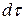 к площадке A1 B1 C1 D1 подведено
к площадке A1 B1 C1 D1 подведено
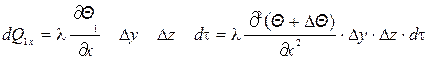 .
.
Учитывая, что 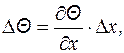 запишем
запишем
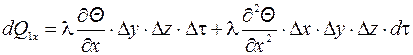 (1.8)
(1.8)
За это же время через площадку ABCD отводится 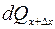 теплоты.
теплоты.
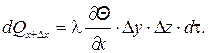 (1.9)
(1.9)
В рассматриваемом объёме остаётся
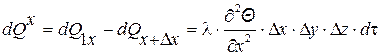 (1.10)
(1.10)
Если положить, что тепло распространяется также по осям Y и Z, то по аналогии можно записать
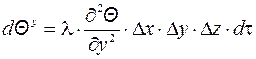 ,
,
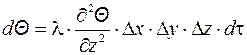 . (1.11)
. (1.11)
Общее же количество тепла для объёмной задачи
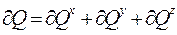 ,
,
или
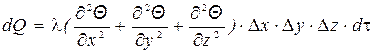 или
или
(1.12)
Разделив левую и правую части выражения (1.12) на 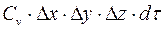 , после преобразования получим
, после преобразования получим
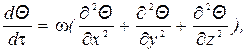 (1.13)
(1.13)
где 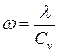 − коэффициент температуропроводности [
− коэффициент температуропроводности [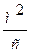 ] характеризует скорость выравнивания температуры в неравномерно нагретом теле. Выражение (1.13) − представляет собой линейное дифференциальное уравнение в частных производных и является классической записью дифференциального уравнения теплопроводности для неподвижной среды.
] характеризует скорость выравнивания температуры в неравномерно нагретом теле. Выражение (1.13) − представляет собой линейное дифференциальное уравнение в частных производных и является классической записью дифференциального уравнения теплопроводности для неподвижной среды.
Для линейного дифференциального уравнения применим принцип суперпозиции, который заключается в том, что общее решение дифференциального уравнения можно получить путём алгебраического суммирования частных решений, когда на тело действуют несколько независимых источников теплоты.
Для двух − или одномерного поля уравнения (1.13) преобразуется к следующему виду
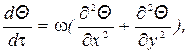 (1.14)
(1.14)
или
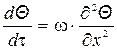 . (1.15)
. (1.15)
Если 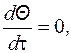 то получим дифференциальное уравнение квазистационарного температурного поля.
то получим дифференциальное уравнение квазистационарного температурного поля.
 . (1.16)
. (1.16)
 2014-02-02
2014-02-02 776
776








