Передаточное отношение цепной передачи:
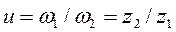 (3.144)
(3.144)
где ω1, ω2, z1 z2 — угловые скорости и числа зубьев ведущей и ведомой звездочек.
Так как 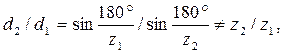 то передаточное отношение и нельзя определять как отношение диаметров делительных окружностей звездочек.
то передаточное отношение и нельзя определять как отношение диаметров делительных окружностей звездочек.
Передаточное отношение, вычисленное по вышеприведенным формулам, является средним за оборот; в пределах поворота звездочки на угловой шаг 360°/z мгновенное передаточное отношение не остается постоянным.
 За один оборот звездочки цепь проходит путь zt, а время одного оборота равно 2π/ω,тогда средняя скорость цепи ν равна
За один оборот звездочки цепь проходит путь zt, а время одного оборота равно 2π/ω,тогда средняя скорость цепи ν равна
 |
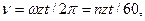 (3.145)
(3.145) где t—шаг цепи; n — частота вращения; ω — угловая скорость звездочки.
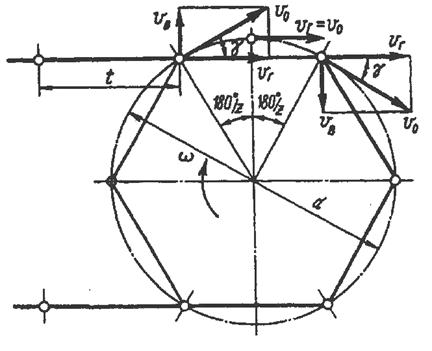
Из схемы цепной передачи (рис. 3.50) видно, что скорость цепи определяется горизонтальной составляющей νг окружной скорости ν0 звездочки, причем
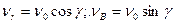 (3.146)
(3.146)
При повороте звездочки на половину углового шага, т. е. на 180°/z, шарнир цепи, находящийся во впадине зуба звездочки, окажется в верхнем положении, вектор окружной скорости займет горизонтальное положение, причем νr = ν0, a νB = 0; при дальнейшем вращении звездочки горизонтальная составляющая νr будет уменьшаться, а вертикальная составляющая νB — увеличиваться, но изменит направление.
Таким образом, за время поворота звездочки на угловой шаг скорость цепи возрастет от значения 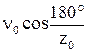 до
до 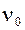 а затем уменьшится до первоначального значения, что приведет к соответствующим изменениям угловой скорости ведомой звездочки и мгновенного передаточного отношения. Вертикальная составляющая νB при этом изменяется в пределах
а затем уменьшится до первоначального значения, что приведет к соответствующим изменениям угловой скорости ведомой звездочки и мгновенного передаточного отношения. Вертикальная составляющая νB при этом изменяется в пределах 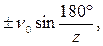 что приводит к соударению шарниров цепи о впадины звездочки, поперечным колебаниям цепи и динамическим нагрузкам на всю передачу.
что приводит к соударению шарниров цепи о впадины звездочки, поперечным колебаниям цепи и динамическим нагрузкам на всю передачу.
Вертикальная составляющая 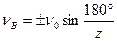 является скоростью удара шарнира и впадины зуба. Очевидно, что с уменьшением числа зубьев звездочки увеличивается скорость и сила ударов, возрастают колебания передаточного отношения и увеличиваются динамические нагрузки в передаче. Кроме того, с уменьшением числа зубьев звездочки увеличивается угол относительного поворота соседних звеньев, что способствует изнашиванию шарниров. Поэтому числа зубьев малой звездочки ограничивают допускаемыми минимальными значениями, несмотря на то, что с уменьшением числа зубьев звездочек уменьшаются габариты передачи.
является скоростью удара шарнира и впадины зуба. Очевидно, что с уменьшением числа зубьев звездочки увеличивается скорость и сила ударов, возрастают колебания передаточного отношения и увеличиваются динамические нагрузки в передаче. Кроме того, с уменьшением числа зубьев звездочки увеличивается угол относительного поворота соседних звеньев, что способствует изнашиванию шарниров. Поэтому числа зубьев малой звездочки ограничивают допускаемыми минимальными значениями, несмотря на то, что с уменьшением числа зубьев звездочек уменьшаются габариты передачи.
Минимальное число зубьев малой звездочки для роликовых и втулочных цепей определяют в зависимости от передаточного числа и по эмпирической формуле:
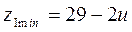 (3.147)
(3.147)
для зубчатых цепей zlmin принимается на 20...30% выше.
Число зубьев большой звездочки z2 ≈ uz1. Следует отметить, что при
нечетном числе зубьев хотя бы одной из звездочек и четном числе звеньев цепи изнашивание зубьев и шарниров более равномерно.
В результате изнашивания шарниров шаг цепи увеличивается и может произойти нарушение работы передачи, когда шарниры будут попадать не во впадину, а на окружность вершины зубьев звездочки, что приводит к соскакиванию или разрыву цепи. Этот процесс резче проявляется на звездочках с большим числом зубьев, поэтому максимальное число зубьев тоже ограничивают: для втулочных и роликовых цепей z2max ≤ 120; для зубчатых цепей z2max ≤ 140 (для стандартных передач z = 17...96).
Плавность, долговечность и бесшумность работы цепной передачи в значительной степени зависят от величины шага цепи; чем меньше шаг, тем меньше динамические нагрузки и выше качество работы передачи. Вместе с тем статическая прочность и нагрузочная способность цепей возрастают с увеличением шага, так как увеличиваются размеры деталей, составляющих шарниры цепи. Поэтому величина шага цепи ограничивается максимально допускаемым значением угловой скорости малой звездочки, указанным в табл. 3.18, где приведены также рекомендуемые для втулочных и роликовых цепей значения угловой скорости.
Ориентировочно оптимальное межосевое расстояние цепной передачи выбирают в зависимости от шага цепи обычно в пределах а = (30...50)t (меньшие значения при малых передаточных числах). Максимальное значение межосевого расстояния ограничивается аmах ≤ 80t во избежание чрезмерного натяжения цепи силой собственной тяжести. Минимальное значение межосевого расстояния
ограничивается условием обеспечения угла обхвата цепью меньшей звездочки
α≥ 120°; аmin ≈ 25t.


При оптимальном межосевом расстоянии ведущая ветвь цепи может располагаться над ведомой или под нею; при значениях, близких к максимальным или минимальным, ведущая ветвь должна находиться над ведомой во избежание соприкосновения ветвей или захлестывания лишних зубьев провисающей ведомой ветвью.
Число звеньев цепи предварительно определяется по формуле
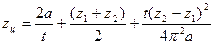 (3.148)
(3.148)
Чтобы не применять переходное звено (см. рис. 3.49), расчетное число звеньев цепи должно быть округлено до четного числа.
Длина цепи
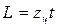 (3,149)
(3,149)
Окончательное значение межосевого расстояния равно
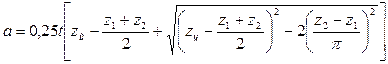 (3.150)
(3.150)
В передачах с нерегулируемым межосевым расстоянием для обеспечения необходимого провисания цепи устанавливают монтажное межосевое расстояние, которое меньше расчетного на (0,002...0,004)а; при значительной вытяжке цепи за счет износа шарниров удаляют необходимое количество звеньев.
Для компенсации удлинения цепи опоры одного из валов иногда делают регулируемыми или применяют оттяжные звездочки или нажимные ролики, которые ставят на ведомую ветвь цепи. Стрела провисания допускается до 0,02a при угле наклона передачи к горизонту до 40° включительно и до 0,015а — при наклоне свыше 40°, где а — межосевое расстояние.
 2014-02-02
2014-02-02 1798
1798
