Кинетика коагуляции
Для начала коагуляции необходимо, чтобы частицы преодолели энергетический барьер Δ Uк и попали в первый минимум. Для этого необходимо уменьшить силы отталкивания, т.е. снизить ς-потенциал, например, за счет введения электролита. Если скорость коагуляции зависит от концентрации электролита, то идет медленная коагуляция. Потенциальный барьер исчезает при пороговой концентрации электролита. После этого скорость коагуляции не зависит от концентрации электролита, т.е. идет быстрая коагуляция.
Процесс коагуляции включает две последовательные стадии:
1) диффузия (сближение частиц);
2) агрегирование (укрупнение частиц).
При быстрой коагуляции каждое столкновение частиц приводит к их слипанию, поэтому скорость быстрой коагуляции определяется только диффузионной стадией. При медленной коагуляции к слипанию частиц приводят не все соударения. Скорость медленной коагуляции зависит как от диффузии частиц, так и от их взаимодействия.
Основные положения:
1. Частицы монодисперсны и имеют сферическую форму.
2. Частицы дисперсной фазы имеют коллоидные размеры и перемещаются за счет броуновского движения.
3. Силы взаимодействия между частицами не учитываются.
4. Все столкновения частиц являются эффективными, т.е. каждое столкновение приводит к слипанию.
5. Учитывается взаимодействие только двух частиц, одновременное взаимодействие трех и более частиц считается маловероятным, т.е. кинетика коагуляции подобна кинетике химической реакции второго порядка.
Уравнение скорости реакции второго порядка:
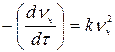 ,
,
где k – константа скорости коагуляции.
Разделим переменные и проинтегрируем в интервале от 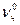 до
до 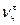 и от 0 до τ:
и от 0 до τ:
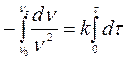 ,
,
где τ – время; ν0 – концентрация частиц до начала коагуляции (τ = 0);
ντ – концентрация частиц в момент времени τ.
В результате интегрирования получаем
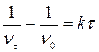 (*)
(*)
Преобразуем уравнение. Умножим левую и правую часть на ν0 и решим уравнение относительно ν0/ντ:
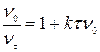 .
.
Приведем уравнение к виду:
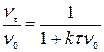 .
.
Получили уравнение Смолуховского.
Из полученного уравнения легко получить формулу для расчета численной концентрации частиц в момент времени τ:
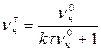
и формулу для расчета константы скорости:
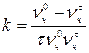 .
.
Часто для характеристики быстрой коагуляции используют время половинной коагуляции Θ – время, за которое начальная численная концентрация снизится в два раза:
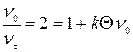
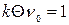
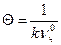
С учетом этого уравнение Смолуховского примет вид:
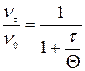
 2014-02-02
2014-02-02 10139
10139