Пример 1 (Рис.44). Построить точку пересечения прямой 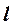 плоскостью
плоскостью 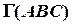 .
.
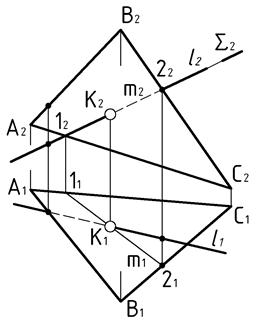 |
| Рис.44 |
Дано: Прям. 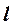 Пл. Пл.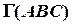 | Решение: 1)  , 2) , 2) 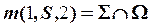 , 3) , 3) 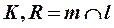 , , 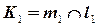 , , 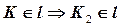 . 4) Видимость. . 4) Видимость. |
?: 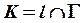 . . |
Проведя через заданную прямую 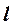 посредник
посредник 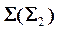 определяем его пересечение с плоскостью
определяем его пересечение с плоскостью 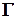 по прямой
по прямой 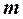 . Для нахождения искомой точки K пересекаем вспомогательную линию
. Для нахождения искомой точки K пересекаем вспомогательную линию 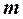
 с заданной -
с заданной - 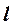 . Построение точки K начинается с горизонтальной проекции.
. Построение точки K начинается с горизонтальной проекции.
Видимость проекций прямой 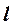 определяется по отмеченным на чертеже конкурирующим точкам.
определяется по отмеченным на чертеже конкурирующим точкам.
Дано: Кон. 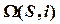 , Пр. , Пр. 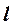 | Решение: 1) 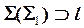 , 2) , 2) 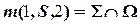 , 3) , 3) 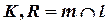 : : 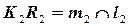 , , 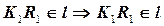 , 4) Видимость. , 4) Видимость. |
?: 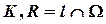 . . |
Пример 2 (Рис.45). Построить точки пересечения прямой 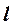 с конусом вращения
с конусом вращения 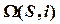 .
.
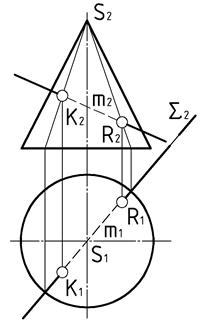 |
| Рис.45 |
Посредник 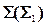 , проведенный через заданную прямую
, проведенный через заданную прямую 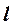 , пересекает конус по ломаной линии
, пересекает конус по ломаной линии 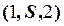 . Места пересечения прямой
. Места пересечения прямой 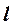 с полученным сечением конуса определяют искомые точки
с полученным сечением конуса определяют искомые точки 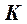 и
и 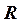 . Построение этих точек на чертеже начинается с фронтальных проекций.
. Построение этих точек на чертеже начинается с фронтальных проекций.
Видимость горизонтальной проекции линии 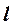 - очевидна. Видимость на фронтальной плоскости проекций определяется видимостью проекций искомых точек пересечения
- очевидна. Видимость на фронтальной плоскости проекций определяется видимостью проекций искомых точек пересечения 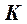 и
и 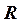 .
.
Пример 3 (Рис.46). Построить линию пересечения плоскостей 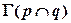 и
и 
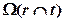 .
.
Дано: Пл. 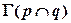 Пл. Пл. 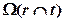 ?: ?: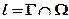 | Решение: | |
1). 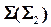 , , | 4). 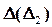 , , | – посредник. |
2). 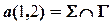 , , 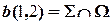 , , | 5). 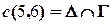 , , 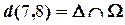 , , | – вспомогательные прямые. |
3). 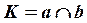 , , | 6). 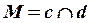 , , | – точка линии пересечения. |
7)  . . | – линия пересечения. |
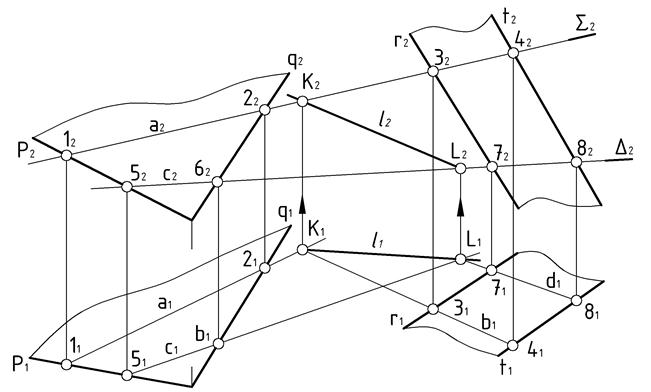 |
| Рис.46 |
При произвольном задании проецирующих посредников, как это было сделано в данной задаче, для построения линии пересечения плоскостей приходиться проводить 4 вспомогательные линии по 8-ми точкам. Для сокращения трудоемкости графических построений следует по возможность задавать посредники параллельными между собой и проводить их через прямые, принадлежащие заданным плоскостям по условию задачи:
| № | Посредники | Линии | Точки |
| Произвольно расположенные | |||
| Параллельные | |||
| Параллельные и использующие заданные каркасы плоскостей |
Те же результаты можно видеть на Рис.47/
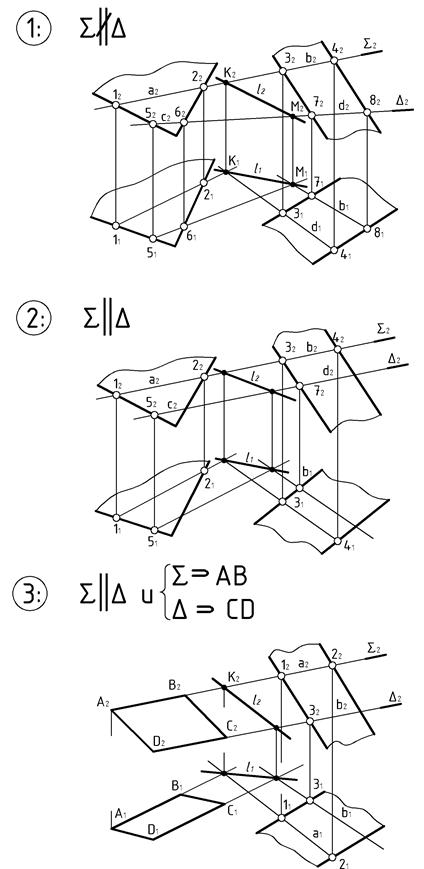 |
| Рис.47 |
Пример 4 (Рис.48). Построить линию пересечения закрытого тора и полусферы.
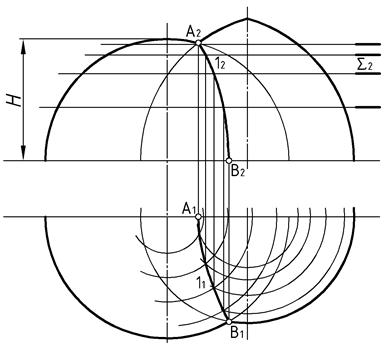 |
| Рис.48 |
Горизонтальные проецирующие секущие плоскости пересекают заданные поверхности по вспомогательным окружностям с простыми проекциями. Пересекаясь попарно окружности определяют точки, принадлежащие линии пересечения заданных поверхностей. Обычный алгоритм решения. Напомним только и дополним последовательность решения задач на пересечение поверхностей применительно к способу проецирующих секущих плоскостей:
1) Выбрать способ решения задачи.
2) Построить опорные точки линии пересечения любым способом и обозначить их буквами. (В данном случае – это самая высокая точка 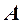 и точка
и точка 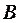 на основании поверхностей).
на основании поверхностей).
3) Ограничить опорными точками область применения посредников (размер 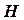 в данной задаче).
в данной задаче).
4) Построить необходимое число промежуточных точек линии пересечения выбранным методом и при необходимости обозначить их цифрами.
5) Построить линию пересечения.
6) Обвести чертеж в целом с учетом видимости.
 2014-02-02
2014-02-02 1479
1479








